题目内容
设x,y为正实数, ,
, ,c=x+y.
,c=x+y.(Ⅰ)如果p=1,则是否存在以a,b,c为三边长的三角形?请说明理由;
(Ⅱ)对任意的正实数x,y,试探索当存在以a,b,c为三边长的三角形时的取值范围.
【答案】分析:(Ⅰ)通过p=1利用三角形两边之和大于第三边,两边之差小于第三边,判断三角形的存在情况.
(Ⅱ)存在以a,b,c为三边长的三角形时,通过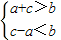 ,利用换元法,构造法,利用基本不等式求出p的范围.
,利用换元法,构造法,利用基本不等式求出p的范围.
解答:解:(Ⅰ)存在.
当p=1时,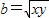 ,
,
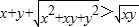 显然成立,
显然成立,
且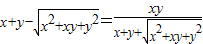 <xy,易知a<c,由上得
<xy,易知a<c,由上得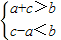 ,
,
故当p=1时,存在以a,b,c为三边长的三角形.
(Ⅱ)∵a<c,∴若存在以a,b,c为三边长的三角形时,只需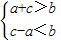 ,
,
即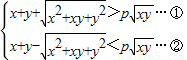
不等式①②两边都除以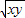 ,令
,令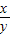 =t,得
=t,得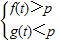 ,这里f(t)=
,这里f(t)=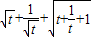 ,
,
g(t)=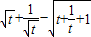 ,
,
由于f(t)=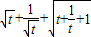 ≥2+
≥2+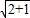 =2+
=2+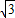 ,
,
当且仅当t=1时,f(t)取最小值2+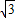 ,令m=
,令m=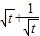 ,
,
则m≥2,g(t)=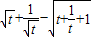 =m-
=m-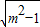 ,
,
易知函数φ(m)=m-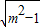 在[2,+∞)上单调递减,
在[2,+∞)上单调递减,
故φ(m)max=2-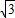 ,即g(t)≤2-
,即g(t)≤2-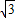 ,当且仅当t=1时,g(t)取最大值2-
,当且仅当t=1时,g(t)取最大值2-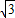 ;
;
因此p的取值范围为2-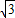 <p<2+
<p<2+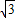 .
.
即p的取值范围为2-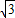 <p<2+
<p<2+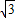 时,存在以a、b、c为三边长的三角形.
时,存在以a、b、c为三边长的三角形.
点评:本题考查三角形的形状的判断,基本不等式的应用,换元法的应用,函数的最值,考查分析问题解决问题,转化思想的应用.
(Ⅱ)存在以a,b,c为三边长的三角形时,通过
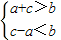 ,利用换元法,构造法,利用基本不等式求出p的范围.
,利用换元法,构造法,利用基本不等式求出p的范围.解答:解:(Ⅰ)存在.
当p=1时,
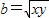 ,
,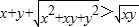 显然成立,
显然成立,且
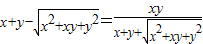 <xy,易知a<c,由上得
<xy,易知a<c,由上得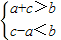 ,
,故当p=1时,存在以a,b,c为三边长的三角形.
(Ⅱ)∵a<c,∴若存在以a,b,c为三边长的三角形时,只需
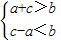 ,
,即
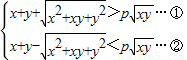
不等式①②两边都除以
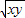 ,令
,令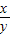 =t,得
=t,得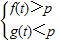 ,这里f(t)=
,这里f(t)=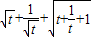 ,
,g(t)=
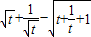 ,
,由于f(t)=
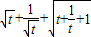 ≥2+
≥2+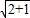 =2+
=2+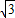 ,
,当且仅当t=1时,f(t)取最小值2+
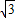 ,令m=
,令m=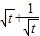 ,
,则m≥2,g(t)=
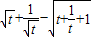 =m-
=m-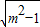 ,
,易知函数φ(m)=m-
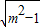 在[2,+∞)上单调递减,
在[2,+∞)上单调递减,故φ(m)max=2-
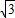 ,即g(t)≤2-
,即g(t)≤2-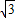 ,当且仅当t=1时,g(t)取最大值2-
,当且仅当t=1时,g(t)取最大值2-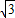 ;
;因此p的取值范围为2-
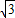 <p<2+
<p<2+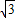 .
.即p的取值范围为2-
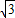 <p<2+
<p<2+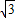 时,存在以a、b、c为三边长的三角形.
时,存在以a、b、c为三边长的三角形.点评:本题考查三角形的形状的判断,基本不等式的应用,换元法的应用,函数的最值,考查分析问题解决问题,转化思想的应用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目