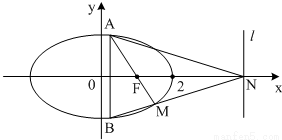
题目内容
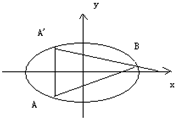 如图,椭圆C:
如图,椭圆C: (a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为
(a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为 .
.
(Ⅰ)求椭圆C的方程.
(Ⅱ)过(1,0)点的直线L与椭圆C交于A,B两点,点A关于x轴的对称点A′(A′与B不重合),求证直线A′B与x轴交于一个定点,求此点坐标.
(Ⅰ)解:∵椭圆C: (a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为
(a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为 ,
,
∴
∵b2=a2-c2
∴
∴a=2
∴椭圆C的方程为 ;
;
(Ⅱ)证明:设直线AB的方程为y=k(x-1),A(x1,y1),B(x2,y2),则A′(x1,-y1),
直线AB的方程代入椭圆方程可得(1+4k2)x2-8k2x+k2-4=0
∴x1+x2=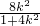 ,
,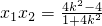
又直线A′B的方程为y-y2=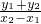 (x-x2)
(x-x2)
令y=0可得x=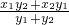 =
= =
= =4
=4
∴直线A′B与x轴交于一个定点,坐标为(4,0).
分析:(Ⅰ)根据椭圆C: (a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为
(a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为 ,建立方程组,结合b2=a2-c2,即可求椭圆C的方程;
,建立方程组,结合b2=a2-c2,即可求椭圆C的方程;
(Ⅱ)设出点的坐标,直线AB的方程,代入椭圆方程,可得直线A′B的方程,利用韦达定理,即可证得结论.
点评:本题考查椭圆的标准方程,考查椭圆的几何性质,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.
 (a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为
(a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为 ,
,∴

∵b2=a2-c2
∴

∴a=2
∴椭圆C的方程为
 ;
;(Ⅱ)证明:设直线AB的方程为y=k(x-1),A(x1,y1),B(x2,y2),则A′(x1,-y1),
直线AB的方程代入椭圆方程可得(1+4k2)x2-8k2x+k2-4=0
∴x1+x2=
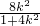 ,
,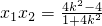
又直线A′B的方程为y-y2=
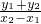 (x-x2)
(x-x2)令y=0可得x=
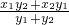 =
= =
= =4
=4∴直线A′B与x轴交于一个定点,坐标为(4,0).
分析:(Ⅰ)根据椭圆C:
 (a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为
(a>b>0),经过点(0,1),椭圆上点到焦点的最远距离为 ,建立方程组,结合b2=a2-c2,即可求椭圆C的方程;
,建立方程组,结合b2=a2-c2,即可求椭圆C的方程;(Ⅱ)设出点的坐标,直线AB的方程,代入椭圆方程,可得直线A′B的方程,利用韦达定理,即可证得结论.
点评:本题考查椭圆的标准方程,考查椭圆的几何性质,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,椭圆C:
如图,椭圆C: ,0),离心率e=
,0),离心率e= ,过点A(0,-2)且不与y轴重合的直线l与椭圆C相交于不同的两点P、Q
,过点A(0,-2)且不与y轴重合的直线l与椭圆C相交于不同的两点P、Q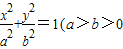 ,a,b为常数),动圆
,a,b为常数),动圆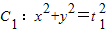 ,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点.
,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点. 与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: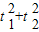 为定值.
为定值.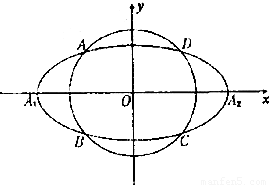
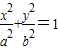 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).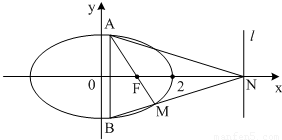
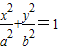 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).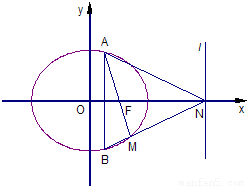
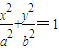 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).