题目内容
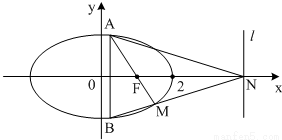
 如图,椭圆C:
如图,椭圆C: (a>b>0)的一个焦点是F(-
(a>b>0)的一个焦点是F(- ,0),离心率e=
,0),离心率e= ,过点A(0,-2)且不与y轴重合的直线l与椭圆C相交于不同的两点P、Q
,过点A(0,-2)且不与y轴重合的直线l与椭圆C相交于不同的两点P、Q
(1)求椭圆C的方程;
(2)若点F到直线l的距离为2,求直线l的方程;
(3)问在y轴上是否存在一个定点B,使得直线PB与椭圆C的另一个交点R是点Q关于y轴的对称点?若存在,求出定点B的坐标;若不存在,请说明理由.
解:(1)∵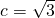 ,
, ,
,
∴a=2,b=1,
∴椭圆方程为 .
.
(2)设直线l的方程为y=kx-2,
由 ,
,
得(1+4k2)x2-16kx+12=0,①
∵△=(16k)2-48(1+4k2)>0,得 或
或 .②
.②
设p(x1,y1),Q(x2,y2),
则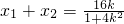 ,
,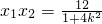 ,
,
由已知得, ,解得k=0,或
,解得k=0,或 ,
,
由②得, ,
,
∴直线l的方程是 .
.
(3)假设y轴上存在定点B,使R与点Q关于y轴对称,则R(-x2,y2),
∴直线PR的方程为 ,
,
令x=0,则 +y1
+y1
=
=
=
=
=
=- .
.
∴存在y轴上定点B ,
,
使得直线PB与椭圆C的另一个交点R是点Q关于y轴的对称点.
分析:(1)由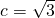 ,
, ,能求出椭圆方程.
,能求出椭圆方程.
(2)设直线l的方程为y=kx-2,由 ,得(1+4k2)x2-16kx+12=0,由△=(16k)2-48(1+4k2)>0,得
,得(1+4k2)x2-16kx+12=0,由△=(16k)2-48(1+4k2)>0,得 或
或 .设p(x1,y1),Q(x2,y2),则
.设p(x1,y1),Q(x2,y2),则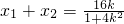 ,
,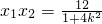 ,由已知得
,由已知得 ,由此能求出直线l的方程.
,由此能求出直线l的方程.
(3)假设y轴上存在定点B,使R与点Q关于y轴对称,则R(-x2,y2),所以直线PR的方程为 ,令x=0,得y=-
,令x=0,得y=- ,所以存在y轴上定点B
,所以存在y轴上定点B ,使得直线PB与椭圆C的另一个交点R是点Q关于y轴的对称点.
,使得直线PB与椭圆C的另一个交点R是点Q关于y轴的对称点.
点评:本题主要考查直线与直线、直线与椭圆的位置关系等基础知识;考查运算求解能力、推理论证能力以及公析与解决问题能力;考查数形结合思想、函数与方程思想、转化思想.
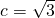 ,
, ,
,∴a=2,b=1,
∴椭圆方程为
 .
.(2)设直线l的方程为y=kx-2,
由
 ,
,得(1+4k2)x2-16kx+12=0,①
∵△=(16k)2-48(1+4k2)>0,得
 或
或 .②
.②设p(x1,y1),Q(x2,y2),
则
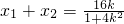 ,
,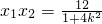 ,
,由已知得,
 ,解得k=0,或
,解得k=0,或 ,
,由②得,
 ,
,∴直线l的方程是
 .
.(3)假设y轴上存在定点B,使R与点Q关于y轴对称,则R(-x2,y2),
∴直线PR的方程为
 ,
,令x=0,则
 +y1
+y1=

=

=

=

=

=-
 .
.∴存在y轴上定点B
 ,
,使得直线PB与椭圆C的另一个交点R是点Q关于y轴的对称点.
分析:(1)由
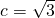 ,
, ,能求出椭圆方程.
,能求出椭圆方程.(2)设直线l的方程为y=kx-2,由
 ,得(1+4k2)x2-16kx+12=0,由△=(16k)2-48(1+4k2)>0,得
,得(1+4k2)x2-16kx+12=0,由△=(16k)2-48(1+4k2)>0,得 或
或 .设p(x1,y1),Q(x2,y2),则
.设p(x1,y1),Q(x2,y2),则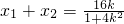 ,
,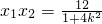 ,由已知得
,由已知得 ,由此能求出直线l的方程.
,由此能求出直线l的方程.(3)假设y轴上存在定点B,使R与点Q关于y轴对称,则R(-x2,y2),所以直线PR的方程为
 ,令x=0,得y=-
,令x=0,得y=- ,所以存在y轴上定点B
,所以存在y轴上定点B ,使得直线PB与椭圆C的另一个交点R是点Q关于y轴的对称点.
,使得直线PB与椭圆C的另一个交点R是点Q关于y轴的对称点.点评:本题主要考查直线与直线、直线与椭圆的位置关系等基础知识;考查运算求解能力、推理论证能力以及公析与解决问题能力;考查数形结合思想、函数与方程思想、转化思想.

练习册系列答案
相关题目
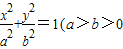 ,a,b为常数),动圆
,a,b为常数),动圆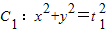 ,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点.
,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点. 与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: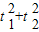 为定值.
为定值.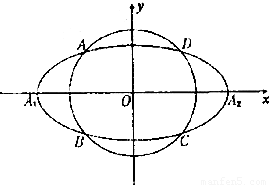
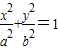 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).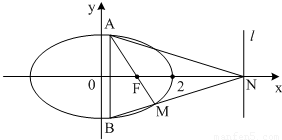
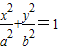 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).
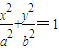 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).