题目内容
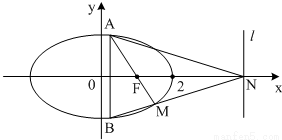
如图,椭圆C: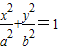 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).(Ⅰ)求椭圆C的方程;
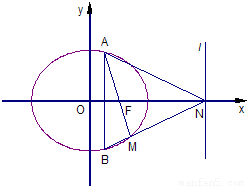
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.
【答案】分析:(I)根据题意,可得a=2且c=1,利用平方关系算出b2=3,因此可求出椭圆C的方程;
(II)(ⅰ)根据题意,得F(1,0),N(4,0).设A(m,n),则B(m,-n),可得AF、BN以m、n为参数的方程,联解得出M(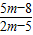 ,
,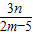 ),再M坐标代入椭圆方程加以验证,即可得到点M恒在椭圆C上;
),再M坐标代入椭圆方程加以验证,即可得到点M恒在椭圆C上;
(ii)设AM的方程为x=ty+1,与椭圆方程消去x得(3t2+4)y2+6ty-9=0.设A(x1,y1),M(x2,y2),由韦达定理将y1+y2、y1y2表示为关于t的式子,从而可得|y1-y2|=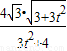 ,然后换元:令3t2+4=λ (λ≥4),可得|y1-y2=4
,然后换元:令3t2+4=λ (λ≥4),可得|y1-y2=4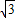 •
•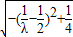 ,根据二次函数的性质算出当
,根据二次函数的性质算出当 =
= 时即t=0时,|y1-y2|取得最大值3,由此可得△AMN面积的最大值为
时即t=0时,|y1-y2|取得最大值3,由此可得△AMN面积的最大值为 .
.
解答:解:(I)由题意得a=2且c=1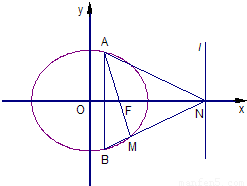
∴为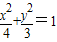
(II)(ⅰ)根据题意,得F(1,0),N(4,0)
设A(m,n),则B(m,-n) (n≠0)
可得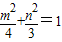
∵AF、BN方程分别为m(x-1)-(m-1)y=0
和m(x-4)-(m-4)y=0
∴M(x,y)满足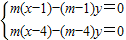 ,
,
联解得x=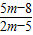 ,y=
,y=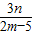
由于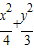 =
=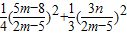 =
=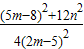 =
=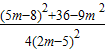 =1
=1
所以点M恒在椭圆C上;
(ii)设AM的方程为x=ty+1,与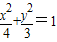 消去x得(3t2+4)y2+6ty-9=0
消去x得(3t2+4)y2+6ty-9=0
设A(x1,y1),M(x2,y2),可得y1+y2= ,y1y2=
,y1y2=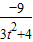
∴|y1-y2|2=(y1+y2)2-4y1y2=(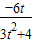 )2+
)2+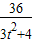 =
=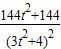
可得|y1-y2|=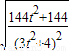 =
=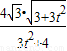
令3t2+4=λ (λ≥4),可得|y1-y2|=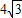 •
•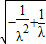 =4
=4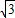 •
•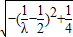
∵λ≥4,可得 ∈(0,
∈(0, ],
],
∴当 =
= 时,即t=0时,|y1-y2|取得最大值3,此时AM经过点F
时,即t=0时,|y1-y2|取得最大值3,此时AM经过点F
∵△AMN面积S= |FN|•|y1-y2|=
|FN|•|y1-y2|= |y1-y2|
|y1-y2|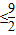
∴当t=0时,即直线AB与x轴垂直时,△AMN面积的最大值为 .
.
点评:本题给出椭圆满足的条件,求椭圆的方程,并求证直线经过定点、求△AMN面积的最大值.着重考查了椭圆的标准方程与简单几何性质、直线与圆锥曲线位置关系等知识,属于中档题.
(II)(ⅰ)根据题意,得F(1,0),N(4,0).设A(m,n),则B(m,-n),可得AF、BN以m、n为参数的方程,联解得出M(
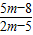 ,
,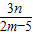 ),再M坐标代入椭圆方程加以验证,即可得到点M恒在椭圆C上;
),再M坐标代入椭圆方程加以验证,即可得到点M恒在椭圆C上;(ii)设AM的方程为x=ty+1,与椭圆方程消去x得(3t2+4)y2+6ty-9=0.设A(x1,y1),M(x2,y2),由韦达定理将y1+y2、y1y2表示为关于t的式子,从而可得|y1-y2|=
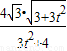 ,然后换元:令3t2+4=λ (λ≥4),可得|y1-y2=4
,然后换元:令3t2+4=λ (λ≥4),可得|y1-y2=4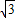 •
•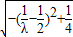 ,根据二次函数的性质算出当
,根据二次函数的性质算出当 =
= 时即t=0时,|y1-y2|取得最大值3,由此可得△AMN面积的最大值为
时即t=0时,|y1-y2|取得最大值3,由此可得△AMN面积的最大值为 .
.解答:解:(I)由题意得a=2且c=1

∴为
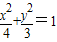
(II)(ⅰ)根据题意,得F(1,0),N(4,0)
设A(m,n),则B(m,-n) (n≠0)
可得
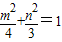
∵AF、BN方程分别为m(x-1)-(m-1)y=0
和m(x-4)-(m-4)y=0
∴M(x,y)满足
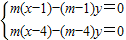 ,
,联解得x=
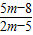 ,y=
,y=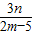
由于
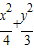 =
=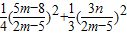 =
=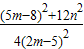 =
=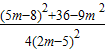 =1
=1所以点M恒在椭圆C上;
(ii)设AM的方程为x=ty+1,与
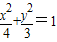 消去x得(3t2+4)y2+6ty-9=0
消去x得(3t2+4)y2+6ty-9=0设A(x1,y1),M(x2,y2),可得y1+y2=
 ,y1y2=
,y1y2=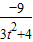
∴|y1-y2|2=(y1+y2)2-4y1y2=(
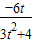 )2+
)2+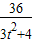 =
=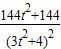
可得|y1-y2|=
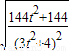 =
=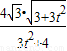
令3t2+4=λ (λ≥4),可得|y1-y2|=
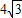 •
•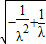 =4
=4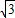 •
•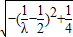
∵λ≥4,可得
 ∈(0,
∈(0, ],
],∴当
 =
= 时,即t=0时,|y1-y2|取得最大值3,此时AM经过点F
时,即t=0时,|y1-y2|取得最大值3,此时AM经过点F∵△AMN面积S=
 |FN|•|y1-y2|=
|FN|•|y1-y2|= |y1-y2|
|y1-y2|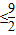
∴当t=0时,即直线AB与x轴垂直时,△AMN面积的最大值为
 .
.点评:本题给出椭圆满足的条件,求椭圆的方程,并求证直线经过定点、求△AMN面积的最大值.着重考查了椭圆的标准方程与简单几何性质、直线与圆锥曲线位置关系等知识,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图,椭圆C:
如图,椭圆C: (a>b>0)的一个焦点是F(-
(a>b>0)的一个焦点是F(- ,0),离心率e=
,0),离心率e= ,过点A(0,-2)且不与y轴重合的直线l与椭圆C相交于不同的两点P、Q
,过点A(0,-2)且不与y轴重合的直线l与椭圆C相交于不同的两点P、Q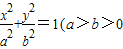 ,a,b为常数),动圆
,a,b为常数),动圆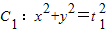 ,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点.
,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点. 与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: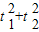 为定值.
为定值.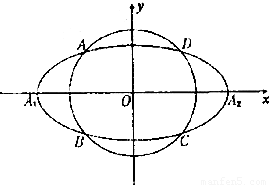
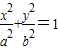 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).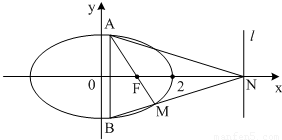
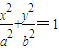 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).