题目内容
6.已知双曲线$\frac{x^2}{9}-\frac{y^2}{16}$=1的左右焦点分别为F1,F2,若双曲线上一点P 满足∠F1PF2=90°,求${S_{△{F_1}P{F_2}}}$=16.分析 先利用双曲线的定义,得|PF1|-|PF2|=±2a=±6,将此式两边平方,再结合勾股定理能求出|PF1|•|PF2|的值,由此能求出△F1PF2的面积.
解答 解:∵双曲线$\frac{x^2}{9}-\frac{y^2}{16}$=1,
∴a=3,b=4,c=$\sqrt{16+9}$=5.
由双曲线的定义,得|PF1|-|PF2|=±2a=±6,
将此式两边平方,得|PF1|2+|PF2|2-2|PF1|•|PF2|=36,
∴|PF1|2+|PF2|2=36+2|PF1|•|PF2|.
又∵∠F1PF2=90°,
∴|PF1|2+|PF2|2=100,
=36+2|PF1|•|PF2|,
∴|PF1|•|PF2|=32,
∴${S_{△{F_1}P{F_2}}}$=$\frac{1}{2}$|PF1|•|PF2|=$\frac{1}{2}$×32=16;
故答案为:16.
点评 本题考查三角形面积的求法,解题时要认真审题,注意双曲线定义、勾股定理的灵活运用,是中档题.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
14.在空间内,可以确定一个平面的条件是( )
| A. | 两两相交的三条直线 | |
| B. | 三条直线,它们两两相交,但不交于同一点 | |
| C. | 三个点 | |
| D. | 三条直线,其中的一条与另外两条直线分别相交 |
11.在平行四边形ABCD中,AB=3,AD=4,则$\overrightarrow{AC}$•($\overrightarrow{AB}$-$\overrightarrow{AD}$)等于( )
| A. | -7 | B. | 1 | C. | 7 | D. | 25 |
16.一个几何体的三视图如图所示,则该几何体的体积是( )
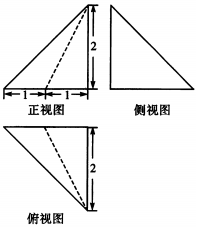

| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |