题目内容
10.不等式组$\left\{\begin{array}{l}{{x}^{2}-x-2>0①}\\{2{x}^{2}+(5+2a)x+5a<0②}\end{array}\right.$解集中的整数有且只有-2,则a的范围( )| A. | [-2,2] | B. | [-2,2) | C. | [-3,2] | D. | [-3,2) |
分析 解x2-x-2>0得:x<-1,或x>2,解2x2+(5+2a)x+5a=0得:x=-$\frac{5}{2}$,或x=-a,结合不等式组$\left\{\begin{array}{l}{{x}^{2}-x-2>0①}\\{2{x}^{2}+(5+2a)x+5a<0②}\end{array}\right.$解集中的整数有且只有-2,可得a的范围.
解答 解:解x2-x-2>0得:x<-1,或x>2,
解2x2+(5+2a)x+5a=0得:x=-$\frac{5}{2}$,或x=-a,
若-a<$-\frac{5}{2}$,则2x2+(5+2a)x+5a<0的解集为:(-a,$-\frac{5}{2}$),
此时不等式组$\left\{\begin{array}{l}{{x}^{2}-x-2>0①}\\{2{x}^{2}+(5+2a)x+5a<0②}\end{array}\right.$的解集为:(-a,$-\frac{5}{2}$),
-2∉(-a,$-\frac{5}{2}$),不满足条件;
若-a=$-\frac{5}{2}$,则2x2+(5+2a)x+5a<0的解集为:∅,
此时不等式组$\left\{\begin{array}{l}{{x}^{2}-x-2>0①}\\{2{x}^{2}+(5+2a)x+5a<0②}\end{array}\right.$的解集为:∅,
-2∉∅,不满足条件;
若-a>$-\frac{5}{2}$,则2x2+(5+2a)x+5a<0的解集为:($-\frac{5}{2}$,-a),
若不等式组$\left\{\begin{array}{l}{{x}^{2}-x-2>0①}\\{2{x}^{2}+(5+2a)x+5a<0②}\end{array}\right.$解集中的整数有且只有-2,
则-2<-a≤3,
解得:a∈[-3,2),
故选:D.
点评 本题考查的知识点是二次不等式的解法,集合的交集运算,分类讨论思想,难度中档.

| A. | f(-2)>f(0)>f(1) | B. | f(-2)>f(1)>f(0) | C. | f(1)>f(0)>f(-2) | D. | f(1)>f(-2)>f(0) |

| A. | $-1-\frac{{\sqrt{2}}}{2}$ | B. | -1 | C. | 0 | D. | $\frac{{\sqrt{2}}}{2}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
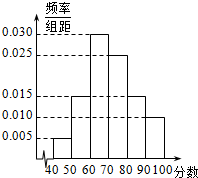 某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.
某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.