题目内容
15.已知正项数列{an}的首项a1=2,点P(an+1,an)在曲线x2-y2=1上.(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_{n+1}}+{a_n}}}$,{bn}的前n项和为Tn,证明:Tn>-2.
分析 (1)由已知得${{a}_{n+1}}^{2}-{{a}_{n}}^{2}=1$,从而{${{a}_{n}}^{2}$}是首项为4,公差为1的等差数列,由此能求出数列{an}的通项公式.
(2)由bn=$\frac{1}{{{a_{n+1}}+{a_n}}}$=$\frac{1}{\sqrt{n+4}+\sqrt{n+3}}$=$\sqrt{n+4}-\sqrt{n+3}$,利用裂项求和法能证明Tn>-2.
解答 (1)解:∵正项数列{an}的首项a1=2,点P(an+1,an)在曲线x2-y2=1上,
∴${{a}_{n+1}}^{2}-{{a}_{n}}^{2}=1$,
又${{a}_{1}}^{2}=4$,∴{${{a}_{n}}^{2}$}是首项为4,公差为1的等差数列,
∴${{a}_{n}}^{2}=4+(n-1)•1$=n+3,
∵正项数列{an}中an>0,
∴an=$\sqrt{n+3}$.
(2)证明:∵bn=$\frac{1}{{{a_{n+1}}+{a_n}}}$=$\frac{1}{\sqrt{n+4}+\sqrt{n+3}}$=$\sqrt{n+4}-\sqrt{n+3}$,
∴Tn=$\sqrt{5}-\sqrt{4}+\sqrt{6}-\sqrt{5}+…+\sqrt{n+4}-\sqrt{n+3}$
=$\sqrt{n+4}-2$>-2,
∴Tn>-2.
点评 本题考查数列的通项公式的求法,考查不等式的证明,是中档题,解题时要认真审题,注意等差数列和裂项求和法的合理运用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
20.函数f(x)是R上的偶函数,且在[0,+∞)上单调递增,则下列各式成立的是( )
| A. | f(-2)>f(0)>f(1) | B. | f(-2)>f(1)>f(0) | C. | f(1)>f(0)>f(-2) | D. | f(1)>f(-2)>f(0) |
7.某程序框图如图所示,则该程序运行后输出的值等于( )
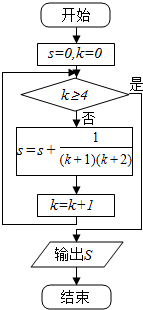

| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
4.已知f(x)=x2-2x,g(x)=x-2,则f[g(2)]与g[f(2)]的大小关系是( )
| A. | f[g(2)]>g[f(2)] | B. | f[g(2)]=g[f(2)] | C. | f[g(2)]<g[f(2)] | D. | 无法确定 |
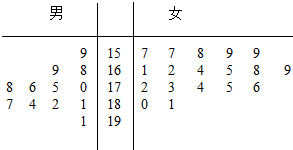 第4届湘台经贸洽谈交流会于2011年6月在我市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.
第4届湘台经贸洽谈交流会于2011年6月在我市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望. 按照新课程的要求,高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.
按照新课程的要求,高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.