题目内容
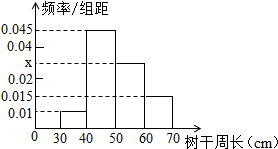
6.某园林局对1000株树木的生长情况进行调查,其中槐树600株,银杏树400株.现用分层抽样方法从这1000株树木中随机抽取100株,其中银杏树树干周长(单位:cm)的抽查结果绘成频率分布直方图如图:(直方图中每个区间仅包含左端点)(1)求直方图中的x值;
(2)若已知树干周长在30cm至40cm之间的4株银杏树中有1株患有虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
分析 ( 1)用分层抽样方法从这1000株树木中随机抽取100株,应该抽取银杏树的株数,由频率分布直方图可得银杏树树干周长在[30,40)、[40,50)、[60,70)分别有多少株,由此能求出直方图中的x值.
(2)记这4株树为树1,树2,树3,树4,且不妨设树4为患虫害的树,记恰好在排查到第二株时发现患虫害树为事件A,则A是指第二次排查到的是树4,由此利用列举法能求出恰好在排查到第二株时发现患虫害的概率.
解答 解:( 1)因为用分层抽样方法从这1000株树木中随机抽取100株,
所以应该抽取银杏树100×$\frac{400}{1000}$=40株,(3分)
由频率分布直方图可得银杏树树干周长在[30,40)、[40,50)、[60,70)分别有4、18、6株,
所以树干周长在[50,60)有40-(4+18+6)=12株,
所以x=$\frac{3}{100}$=0.03.(6分)
(2)记这4株树为树1,树2,树3,树4,且不妨设树4为患虫害的树,
记恰好在排查到第二株时发现患虫害树为事件A,则A是指第二次排查到的是树4,(8分)
因为求恰好在排查到第二株时发现患虫害树的概率,所以基本事件为:
(树1,树2),(树1,树3),(树1,树4),(树2,树1),(树2,树3),(树2,树4),
(树3,树1),(树3,树2),(树3,树4),(树4,树1),(树4,树2),(树4,树3),
共计12个基本事件,(12分)
而事件A中包含的基本事件有(树1,树4),(树2,树4),(树3,树4),共计3个基本事件,
所以恰好在排查到第二株时发现患虫害的概率P(A)=$\frac{3}{12}=\frac{1}{4}$.(14分)
点评 本题考查频率直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | [5a,-2a) | B. | (-∞,5a]∪(-2a,+∞) | C. | (-2a,5a]? | D. | (-∞,5a] |
| A. | $\frac{{π}^{2}}{18}$ | B. | $\frac{{π}^{2}}{9}$ | C. | $\frac{\sqrt{2}}{6}π$ | D. | $\frac{π}{9}$ |
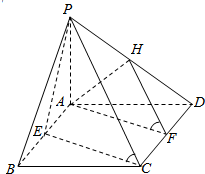 如图所示,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2CD=2,E,F,H分别为AB,CD,PD的中点,求证:(1)平面AFH∥平面PCE;(2)求VD-AHF.
如图所示,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2CD=2,E,F,H分别为AB,CD,PD的中点,求证:(1)平面AFH∥平面PCE;(2)求VD-AHF.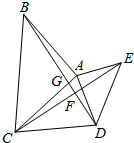 如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,
如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,