题目内容
1.已知四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是正方形,PA=AB=a,E、F分别是边AB、CD的中点.若直线EF被四棱锥的外接球截得的线段长为2$\sqrt{2}$,则该球的体积为4$\sqrt{3}$π.分析 由题意四棱锥P-ABCD的五个顶点位于同一个正方体的顶点处,且与该正方体内接于同一个球.由此结合题意,可得正文体的棱长为2,算出外接球半径R,再结合球的体积公式,即可得到该球体积.
解答 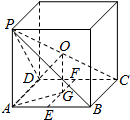 解:由题意四棱锥P-ABCD的五个顶点位于同一个正方体的顶点处,且与该正方体内接于同一个球.
解:由题意四棱锥P-ABCD的五个顶点位于同一个正方体的顶点处,且与该正方体内接于同一个球.
设外接球的球心为O,则O也是正方体的中心,设EF中点为G,连接OG,OA,AG
根据题意,直线EF被球面所截得的线段长为2$\sqrt{2}$,即正方体面对角线长也是2$\sqrt{2}$,
∴得AG=$\sqrt{2}$=$\frac{\sqrt{2}}{2}$a,∴正方体棱长a=2
∴Rt△OGA中,OG=$\frac{1}{2}$a=1,AO=$\sqrt{3}$,
即外接球半径R=$\sqrt{3}$,得外接球的体积为$\frac{4}{3}$πR3=4$\sqrt{3}$π.
故答案为:4$\sqrt{3}$π.
点评 本题主要考查求外接球的体积,着重考查了正方体的性质、三视图和球内接多面体等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.设f(x)=3x+3x-8,现用二分法求方程3x+3x-8=0在区间(1,2)内的近似解的,计算得f(1)<0,f(1.25)<0,f(1.5)>0,f(2)>0,则方程的根落在的区间( )
| A. | (1,1.25) | B. | (1.25,1.5) | C. | (1.5,2) | D. | 不能确定 |
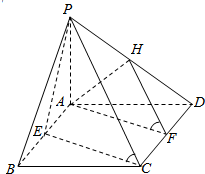 如图所示,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2CD=2,E,F,H分别为AB,CD,PD的中点,求证:(1)平面AFH∥平面PCE;(2)求VD-AHF.
如图所示,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2CD=2,E,F,H分别为AB,CD,PD的中点,求证:(1)平面AFH∥平面PCE;(2)求VD-AHF.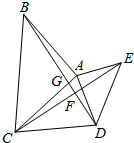 如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,
如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,