题目内容
点P在曲线y=
+x-1上移动，设在点x=1处的切线的倾斜角为α，则α= ．
| 2 |
| x |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数，得到x=1的导数值，由倾斜角的正切值等于斜率得答案．
解答：
解：由y=
+x-1，得y′=-
+1，
∴y′|x=1=-1，
则tanα=-1，∵α∈[0，π），∴α=
．
故答案为：
．
| 2 |
| x |
| 2 |
| x2 |
∴y′|x=1=-1，
则tanα=-1，∵α∈[0，π），∴α=
| 3π |
| 4 |
故答案为：
| 3π |
| 4 |
点评：本题考查了利用导数研究曲线上某点的切线方程，考查了直线倾斜角和斜率的关系，是中低档题．
练习册系列答案
相关题目
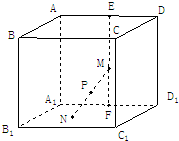如图，在棱长为4的正方体ABCD-A1B1C1D1中，E、F分别是AD，A1D1的中点，长为2的线段MN的一个端点M在线段EF上运动，另一个端点N在底面A1B1C1D1上运动，则线段MN的中点P在二面角A-A1D1-B1内运动所形成的轨迹（曲面）的面积为（ ）| A、4π | ||
| B、π | ||
C、
| ||
| D、2π |
如图所示，向量
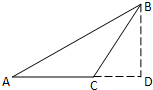已知△ABC为等腰三角形，∠A=∠B=30°，BD为AC边上的高，若| AB |
| a |
| AC |
| b |
| BD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|