题目内容
如图所示,甲船由A岛出发向北偏东45°的方向做匀速直线航行,速度为15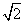 n mile/h,在甲船从A岛出发的同时,乙船从A岛正南40n mile处的B岛出发,朝北偏东θ(θ=arctan
n mile/h,在甲船从A岛出发的同时,乙船从A岛正南40n mile处的B岛出发,朝北偏东θ(θ=arctan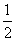 )的方向做匀速直线航行,速度为10
)的方向做匀速直线航行,速度为10 n mile/h.
n mile/h.
(1)求出发后3h两船相距多少海里?
(2)求两船出发后多长时间相距最近?最近距离为多少海里?
(3)两船在航行中能否相遇?试说明理由.

以A为原点,BA所在直线为y轴建立平面直角坐标系.
设在t时刻甲、乙两船分别在P(x1,y1),Q(x2,y2),
则x1=15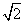 tcos45°=15t,y1=x1=15t,
tcos45°=15t,y1=x1=15t,
由θ=arctan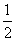 可得,cosθ=
可得,cosθ=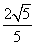 ,sinθ=
,sinθ=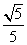 ,
,
故x2=10 tsinθ=10t,
tsinθ=10t,
y2=10 tcosθ-40=20t-40,
tcosθ-40=20t-40,
(1)令t=3,则P、Q两点的坐标分别为(45,45),(30,20),
|PQ|=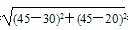 =
=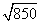 =5
=5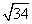 .
.
即两船出发后3h,相距5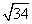 n mile.
n mile.
(2)由(1)的求解过程易知:
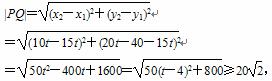 ∴当且仅当t=4时,|PQ|取得最小值20
∴当且仅当t=4时,|PQ|取得最小值20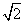 .
.
即两船出发后4h,相距最近,距离为20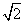 n mile.
n mile.
(3)由(2)知两船航行过程中的最近距离为20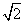 n mile,故两船不可能相遇.
n mile,故两船不可能相遇.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 ),cos(α-
),cos(α- )=
)=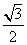 ,sin(
,sin(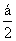 -β)=-
-β)=- ,则cos(α+β)的值等于( )
,则cos(α+β)的值等于( ) =
= ,
, =3,则△ABC的面积为________.
=3,则△ABC的面积为________.
 |=( )
|=( ) (λ∈R),则λ的值为________.
(λ∈R),则λ的值为________. ,
, ) B.(-
) B.(- =( )
=( )
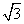 B.
B.
 D.
D.