题目内容
9.已知Sn为等比数列{an}的前n项和,a1=2,且a4-1,a5,3a4+1成等差数列.(1)求数列{an}的通项公式及Sn;
(2)若bn=log2(an•an+1),${c_n}=\frac{1}{{{b_n}•{b_{n+1}}}}$,求数列{cn}的前n项和Tn.
分析 (1)设数列{an}的公比为q,根据题意数列的公比,利用等比数列的通项公式,即可求解数列{an}的通项公式;
(2)由(1)得出bn=2n+5,${c_n}=\frac{1}{2}(\frac{1}{2n+5}-\frac{1}{2n+7})$,利用等差数列求和公式和裂项求和即可求解数列的和.
解答 解:(1)设数列{an}的公比为q,
由题意知3a4=S5-S3=a4+a5,∴a5=2a4,∴q=2.
∴${a_n}={a_1}•{q^{n-1}}={2^{n+2}}$.
(2)由(1)可得bn=n+2+n+3=2n+5,${c_n}=\frac{1}{(2n+5)(2n+7)}=\frac{1}{2}(\frac{1}{2n+5}-\frac{1}{2n+7})$,
∴数列{cn}的前n项和Tn=$\frac{1}{2}[(\frac{1}{7}-\frac{1}{9})+(\frac{1}{9}-\frac{1}{11})$+…+$(\frac{1}{2n+5}-\frac{1}{2n+7})]$=$\frac{n}{14n+49}$.
点评 本题考查了等差数列与等比数列的通项公式及其求和公式、“裂项求和”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
19.四面体ABCD的各棱长均为2,且四个顶点都在一个球面上,则该球的表面积为( )
| A. | 6π | B. | $\sqrt{6}π$ | C. | $\frac{3}{2}π$ | D. | 24π |
4.已知$\overrightarrow a$,$\overrightarrow b$是非零向量,且向量$\overrightarrow a$,$\overrightarrow b$的夹角为$\frac{π}{3}$,若向量$\overrightarrow p=\frac{\overrightarrow a}{|\overrightarrow a|}+\frac{\overrightarrow b}{|\overrightarrow b|}$,则$|\overrightarrow p|$=( )
| A. | $2+\sqrt{3}$ | B. | $\sqrt{2+\sqrt{3}}$ | C. | 3 | D. | $\sqrt{3}$ |
10.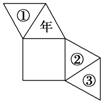 某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
 某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )| A. | 快、新、乐 | B. | 乐、新、快 | C. | 新、乐、快 | D. | 乐、快、新 |
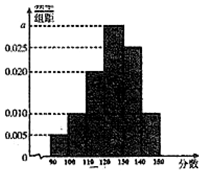 某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.
某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.