题目内容
若loga(a+1)<0(a>0,且a≠1),则函数f(x)=
的定义域为( )
| 1 | ||
|
| A、(-∞,0) |
| B、(-1,0) |
| C、(0,+∞) |
| D、(0,1) |
考点:对数函数的单调性与特殊点,函数的定义域及其求法
专题:函数的性质及应用
分析:根据对数函数的性质对a进行分类讨论,分别利用对数、指数函数的单调性求出函数f(x)的定义域.
解答:
解:当0<a<1时,由loga(a+1)<0得,loga(a+1)<
,
所以a+1>1,解得a>0,则0<a<1,
由1-ax>0得,x>0,
所以函数f(x)=
的定义域为(0,+∞);
当a>1时,由loga(a+1)<0得,loga(a+1)<
,
所以a+1<1,解得a<0,则a无解,
综上得,函数f(x)=
的定义域为(0,+∞),
故选:C.
| log | 1 a |
所以a+1>1,解得a>0,则0<a<1,
由1-ax>0得,x>0,
所以函数f(x)=
| 1 | ||
|
当a>1时,由loga(a+1)<0得,loga(a+1)<
| log | 1 a |
所以a+1<1,解得a<0,则a无解,
综上得,函数f(x)=
| 1 | ||
|
故选:C.
点评:本题考查对数、指数函数的性质,以及分类讨论思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△OAB中,|
|=a,|
|=b,OD是AB边上的高,若
=λ
,则实数λ等于( )
| OA |
| OB |
| AD |
| AB |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
下列赋值语句正确的是( )
| A、x+y=y-2 |
| B、m=m+1 |
| C、m-n=2 |
| D、5=x |
直线y=ax+b(a+b=0)的图象可能是( )
A、 |
B、 |
C、 |
D、 |
已知直线l1:2y=x+2与直线l2:y+2x+1=0,则l1与l2的位置关系为( )
| A、相交不垂直 | B、相交且垂直 |
| C、平行不重合 | D、重合 |
若圆(x-5)2+(y-1)2=r2上有且仅有两点到直线4x+3y+2=0的距离等于1,则r的取值范围为( )
| A、[4,6] |
| B、(4,6) |
| C、[5,7] |
| D、(5,7) |
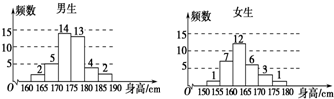 为了解学生身高情况,某校以10%的比例对高三年级的700名学生按性别进行分层抽样调查,测得身高情况的统计图如图:
为了解学生身高情况,某校以10%的比例对高三年级的700名学生按性别进行分层抽样调查,测得身高情况的统计图如图: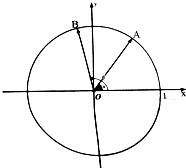 如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别于单位圆交于A,B两点,
如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别于单位圆交于A,B两点,