题目内容
1.设b和c分别是先后抛掷一颗骰子得到的点数,则方程x2-bx+c=0有实根的概率为$\frac{19}{36}$.分析 由已知b2-4c≥0,b和c分别是先后抛掷一颗骰子得到的点数,基本事件总数n=6×6=36,再用列举法求出方程x2-bx+c=0有实根,即b2≥4c包含的基本事件个数,由此能求出方程x2-bx+c=0有实根的概率.
解答 解:∵方程x2-bx+c=0有实根,
∴△=(-b)2-4c=b2-4c≥0,
∵b和c分别是先后抛掷一颗骰子得到的点数,
∴基本事件总数n=6×6=36,
方程x2-bx+c=0有实根,即b2≥4c包含的基本事件情况有:
b=2时,c可取1;b=3时,c可取1,2;b=4时,c可取1,2,3,4;
b=5时,c可取1,2,3,4,5,6;b=6时,c可取1,2,3,4,5,6,
∴方程x2-bx+c=0有实根,即b2≥4c包含的基本事件个数m=1+2+4+6+6=19,
∴方程x2-bx+c=0有实根的概率p=$\frac{m}{n}$=$\frac{19}{36}$.
故答案为:$\frac{19}{36}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
12.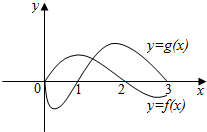 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
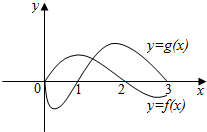 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)<0的解集是( )| A. | (0,1)∪(2,3) | B. | (-2,-1)∪(0,1)∪(2,3) | ||
| C. | (-1,0)∪(-3,-2)∪(0,1)∪(2,3) | D. | (-3,-1)∪(0,1)∪(2,3) |
 是双曲线
是双曲线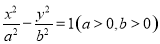 上的三个点,
上的三个点,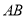 经过原点
经过原点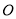 ,
,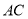 经
经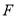 ,若
,若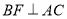 且
且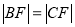 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )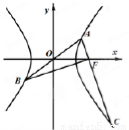
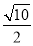 B.
B.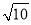 C.
C.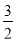 D.
D.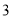
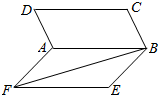 如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.