题目内容
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,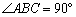 ,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.
,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.
(Ⅰ)求证:AB⊥平面PBC;
(Ⅱ)求平面ADP与平面BCP所成的锐二面角的大小;
 |
(Ⅰ)证明:因为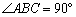 ,所以
,所以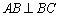 ,
,
因为平面PBC⊥平面ABCD,平面PBC 平面ABCD=BC,AB
平面ABCD=BC,AB 平面ABCD,
平面ABCD,
所以AB⊥平面PBC.
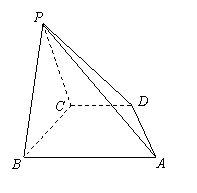
(Ⅱ)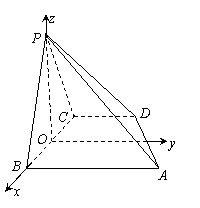 如图,取BC的中点O,连接PO,因为PB=PC,所以PO⊥BC。因为PB=PC,所以PO⊥BC,因为平面PBC⊥平面ABCD,所以PO⊥平面ABCD。以O为原点,OB所在的直线为x轴,在平面ABCD内过O垂直于BC的直线为y轴,OP所在直线为z轴建立空间直角坐标系O-xyz。
如图,取BC的中点O,连接PO,因为PB=PC,所以PO⊥BC。因为PB=PC,所以PO⊥BC,因为平面PBC⊥平面ABCD,所以PO⊥平面ABCD。以O为原点,OB所在的直线为x轴,在平面ABCD内过O垂直于BC的直线为y轴,OP所在直线为z轴建立空间直角坐标系O-xyz。
不妨设BC=2。由AB=PB=PC=BC=2CD得,
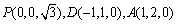 ,
,
所以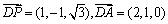 ,
,
设平面PAD的法向量为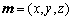 .
.
因为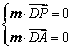 ,所以
,所以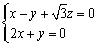 .
.
令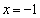 ,则
,则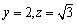 ,所以
,所以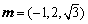 .
.
取平面BCP的一个法向量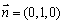 ,
,
所以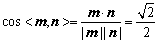 ,
,
所以平面ADP与平面BCP所成的锐二面角的大小为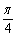 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ______________
______________ 表面积是 。
表面积是 。
 (B)
(B) (C)
(C)  (D)
(D)

 的顶点为
的顶点为 ,与
,与 轴正半轴的交点为
轴正半轴的交点为 ,抛物线与两坐标轴正
,抛物线与两坐标轴正 ,随机往
,随机往 落在△
落在△ 内的概率是 .
内的概率是 . .
. 时,解不等式
时,解不等式 ;
; 时,
时, ,求
,求 的取值范围.
的取值范围. 满足
满足 且
且 ,则向量
,则向量 的夹角是( )
的夹角是( ) B、
B、 C、
C、 D、
D、
 是实数,则“
是实数,则“ ”是 “
”是 “ ” 的
” 的