题目内容
2．已知函数f（x）=-x3+ax在区间[-2，1]上是单调增函数，则实数a的最小值是（ ）| A． | 12 | B． | 0 | C． | 3 | D． | 1 |
分析 求出函数的导数，问题转化为a≥（3x2）max在[-2，1]恒成立，求出a的范围即可．
解答 解：f′（x）=-3x2+a，
若f（x）在[-2，1]递增，
则-3x2+a≥0在[-2，1]恒成立，
即a≥（3x2）max在[-2，1]恒成立，
故a≥12，
故选：A．
点评 本题考查了函数的单调性、最值问题，考查导数的应用以及函数恒成立问题，是一道基础题．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
12．已知$x，y∈[-\frac{π}{4}，\frac{π}{4}]，a∈R$，且x3+sinx-2a=0，4y3+$\frac{1}{2}$sin2y+a=0，则cos（x+2y）的值为（ ）
| A． | 0 | B． | $\frac{1}{4}$ | C． | $-\frac{1}{2}$ | D． | 1 |
10．已知关于x的不等式x2-4ax+3a2＜0（a＞0）的解集为（x1，x2），则${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$的最小值是（ ）
| A． | $\frac{{\sqrt{6}}}{3}$ | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\frac{{4\sqrt{3}}}{3}$ | D． | $-\frac{{4\sqrt{3}}}{3}$ |
17．“ab＜0”是“方程ax2+by2=c表示双曲线”的（ ）
| A． | 充分必要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不必要也不充分条件 |
17．
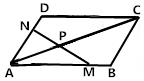如图，在?ABCD中，M，N分别为AB，AD上的点，且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$，$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$，连接AC，MN交于P点，若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$，则λ的值为（ ）
如图，在?ABCD中，M，N分别为AB，AD上的点，且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$，$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$，连接AC，MN交于P点，若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$，则λ的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{7}$ | C． | $\frac{6}{13}$ | D． | $\frac{6}{17}$ |