题目内容
已知两个定圆O1,O2,它们的半径分别是1和2,且|O1O2|=4,动圆M与圆O1内切,又与圆O2外切,建立适当的坐标系,求动圆圆心M的轨迹方程,并说明轨迹是何种曲线.
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:设两个定圆O1(-2,0),O2(2,0),建立坐标系,设动圆圆心为M(x,y),半径为R,由两个圆相内切和外切的条件,写出动圆圆心满足的关系式,由双曲线的定义确定其轨迹即可.
解答:
解:由两个定圆O1,O2,它们的半径分别是1和2,且|O1O2|=4,
设两个定圆O1(-2,0),O2(2,0),建立坐标系,
设动圆圆心为M(x,y),半径为R,
动圆M与圆O1内切,又与圆O2外切,满足|MO1|=R-1,|MO2|=R+2
所以|MO2|-|MO1|=3(常数)且3<4=|O1O2|
故M点的轨迹为以,O1O2为焦点的双曲线的一支.
c=2,a=
,b2=
.
所求轨迹方程为:
-
=1,(x≤-
)
M点的轨迹为以,O1O2为焦点的双曲线的左支.
设两个定圆O1(-2,0),O2(2,0),建立坐标系,
设动圆圆心为M(x,y),半径为R,
动圆M与圆O1内切,又与圆O2外切,满足|MO1|=R-1,|MO2|=R+2
所以|MO2|-|MO1|=3(常数)且3<4=|O1O2|
故M点的轨迹为以,O1O2为焦点的双曲线的一支.
c=2,a=
| 3 |
| 2 |
| 7 |
| 4 |
所求轨迹方程为:
| x2 | ||
|
| y2 | ||
|
| 3 |
| 2 |
M点的轨迹为以,O1O2为焦点的双曲线的左支.
点评:本题考查定义法求轨迹方程、两圆相切的条件等知识,考查利用所学知识解决问题的能力.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
若cos(π+A)=
,那么sin(
π-A)的值为( )
| 1 |
| 3 |
| 3 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
椭圆
+
=1中,以点M(-1,2)为中点的弦所在的直线斜率为( )
| x2 |
| 16 |
| y2 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知a,b∈[-2,2],在此范围内任取数对(a,b),能使函数f(x)=x3-3x+a+b,有三个不同零点的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
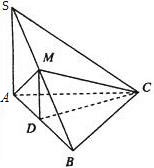 如图所示,三棱锥S-ABC中,SA⊥AC,AC⊥BC,M为SB的中点,D为AB的中点,且△AMB为正三角形.
如图所示,三棱锥S-ABC中,SA⊥AC,AC⊥BC,M为SB的中点,D为AB的中点,且△AMB为正三角形.