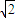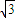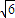题目内容
已知等腰三角形的顶角的余弦值等于-
，则这个三角形底角等于
| 7 |
| 25 |
arcsin
| 3 |
| 5 |
arcsin
（用反三角函数值表示）．| 3 |
| 5 |
分析：设△ABC中 AB=AC，作AD⊥BC于D，设∠CAD=α，则∠ABC=2α．利用二倍角的余弦公式列式，解出cosα=
．进而在Rt△ACD中算出sinC=
，由此即可得到此等腰三角形的底角大小．
| 3 |
| 5 |
| 3 |
| 5 |
解答：解：
设等腰三角形为△ABC，AB=AC，如图所示
作AD⊥BC于D，设∠CAD=α，则∠ABC=2α
∵cos∠ABC=-
，即cos2α=-
∴2cos2α-1=-
，解之得cosα=
（舍负）
因此，Rt△ACD中，sin∠C=cosα=
，可得角C=arcsin
即此等腰三角形的底角等于arcsin
故答案为：arcsin
设等腰三角形为△ABC，AB=AC，如图所示作AD⊥BC于D，设∠CAD=α，则∠ABC=2α
∵cos∠ABC=-
| 7 |
| 25 |
| 7 |
| 25 |
∴2cos2α-1=-
| 7 |
| 25 |
| 3 |
| 5 |
因此，Rt△ACD中，sin∠C=cosα=
| 3 |
| 5 |
| 3 |
| 5 |
即此等腰三角形的底角等于arcsin
| 3 |
| 5 |
故答案为：arcsin
| 3 |
| 5 |
点评：本题给出等腰三角形的顶角大小，叫我们用反三角函数表示底角的大小．着重考查了二倍角的三角函数公式和解三角形等知识，属于中档题．
练习册系列答案
相关题目
已知等腰三角形的面积为
，顶角的正弦值是底角正弦值的
倍，则该三角形一腰的长为（ ）
| ||
| 2 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
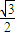，顶角的正弦值是底角正弦值的
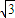倍，则该三角形一腰的长为（ ）
