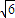题目内容
已知等腰三角形的面积为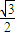 ,顶角的正弦值是底角正弦值的
,顶角的正弦值是底角正弦值的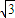 倍,则该三角形一腰的长为( )
倍,则该三角形一腰的长为( )A.
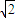
B.
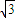
C.2
D.
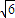
【答案】分析:设出等腰三角形的顶角,表示出等腰三角形的底角,根据顶角的正弦值是底角正弦值的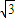 倍列出关系式,利用诱导公式及二倍角的正弦函数公式化简,得到顶角一半的正弦值,利用特殊角的三角函数值求出顶角的度数,又设腰长为m,根据三角形的面积公式表示出三角形的面积S,让面积等于
倍列出关系式,利用诱导公式及二倍角的正弦函数公式化简,得到顶角一半的正弦值,利用特殊角的三角函数值求出顶角的度数,又设腰长为m,根据三角形的面积公式表示出三角形的面积S,让面积等于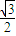 列出关于m的方程,求出方程的解即可得到m的值即为三角形的腰长.
列出关于m的方程,求出方程的解即可得到m的值即为三角形的腰长.
解答:解:设等腰三角形的顶角为α,底角为90°-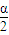 ,腰长为m,m>0,
,腰长为m,m>0,
根据题意得:sinα=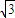 sin(90°-
sin(90°-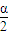 )=
)=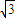 cos
cos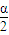 ,即2sin
,即2sin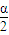 cos
cos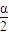 =
=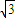 cos
cos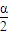 ,
,
解得:sin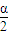 =
=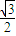 ,
,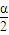 =60°,所以α=120°,
=60°,所以α=120°,
又等腰三角形的面积S= m2sinα=
m2sinα=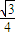 m2=
m2=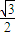 ,即m2=2,m>0,
,即m2=2,m>0,
解得:m=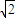 .
.
故选A
点评:此题考查学生灵活运用诱导公式及特殊角的三角函数值化简求值,灵活运用三角形的面积公式化简求值,是一道基础题.
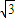 倍列出关系式,利用诱导公式及二倍角的正弦函数公式化简,得到顶角一半的正弦值,利用特殊角的三角函数值求出顶角的度数,又设腰长为m,根据三角形的面积公式表示出三角形的面积S,让面积等于
倍列出关系式,利用诱导公式及二倍角的正弦函数公式化简,得到顶角一半的正弦值,利用特殊角的三角函数值求出顶角的度数,又设腰长为m,根据三角形的面积公式表示出三角形的面积S,让面积等于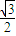 列出关于m的方程,求出方程的解即可得到m的值即为三角形的腰长.
列出关于m的方程,求出方程的解即可得到m的值即为三角形的腰长.解答:解:设等腰三角形的顶角为α,底角为90°-
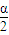 ,腰长为m,m>0,
,腰长为m,m>0,根据题意得:sinα=
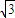 sin(90°-
sin(90°-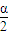 )=
)=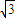 cos
cos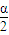 ,即2sin
,即2sin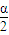 cos
cos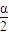 =
=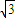 cos
cos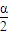 ,
,解得:sin
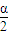 =
=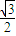 ,
,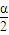 =60°,所以α=120°,
=60°,所以α=120°,又等腰三角形的面积S=
 m2sinα=
m2sinα=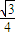 m2=
m2=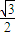 ,即m2=2,m>0,
,即m2=2,m>0,解得:m=
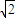 .
.故选A
点评:此题考查学生灵活运用诱导公式及特殊角的三角函数值化简求值,灵活运用三角形的面积公式化简求值,是一道基础题.

练习册系列答案
相关题目
已知等腰三角形的面积为
,顶角的正弦值是底角正弦值的
倍,则该三角形一腰的长为( )
| ||
| 2 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
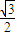 ,顶角的正弦值是底角正弦值的
,顶角的正弦值是底角正弦值的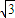 倍,则该三角形一腰的长为( )
倍,则该三角形一腰的长为( )