题目内容
9.若$tanα=\frac{1}{2}$,则$\frac{2sinα+cosα}{4sinα-cosα}$=2.分析 由条件利用同角三角函数的基本关系,求得所给式子的值.
解答 解:若$tanα=\frac{1}{2}$,则$\frac{2sinα+cosα}{4sinα-cosα}$=$\frac{2tanα+1}{4tanα-1}$=$\frac{1+1}{2-1}$=2,
故答案为:2.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.某公司为了解用户对其产品的满意度,从某地区随机调查了100个用户,得到用户对产品的满意度评分频率分布表如下:
(1)根据上面的频率分布表,估计该地区用户对产品的满意度评分超过70分的概率;
(2)请由频率分布表中数据计算众数、中位数,平均数,根据样本估计总体的思想,若平均分低于75分,视为不满意.判断该地区用户对产品是否满意?
| 组别 | 分组 | 频数 | 频率 |
| 第一组 | (50,60] | 10 | 0.1 |
| 第二组 | (60,70] | 20 | 0.2 |
| 第三组 | (70,80] | 40 | 0.4 |
| 第四组 | (80,90] | 25 | 0.25 |
| 第五组 | (90,100) | 5 | 0.05 |
| 合计 | 100 | 1 |
(2)请由频率分布表中数据计算众数、中位数,平均数,根据样本估计总体的思想,若平均分低于75分,视为不满意.判断该地区用户对产品是否满意?
14.小明用流程图把早上上班前需要做的事情做了如图方案,则所用时间最少是( )

| A. | 23分钟 | B. | 24分钟 | C. | 26分钟 | D. | 31分钟 |
18.某青年教师近五年内所带班级的数学平均成绩统计数据如下(满分均为150分):
(Ⅰ)利用所给数据,求出平均分与年份之间的回归直线方程$\widehat{y}$=bx+a,并判断它们之间是正相关还是负相关.
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该教师2016年所带班级的数学平均成绩.
(Ⅲ)能否利用该回归方程估计该教师2030年所带班级的数学平均成绩?为什么?
(b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$)
| 年份x年 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该教师2016年所带班级的数学平均成绩.
(Ⅲ)能否利用该回归方程估计该教师2030年所带班级的数学平均成绩?为什么?
(b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$)
19.已知α∈($\frac{π}{2}$,π),sin(π+α)=-$\frac{3}{5}$,则tan(α-$\frac{π}{4}$)等于( )
| A. | -7 | B. | -$\frac{1}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |
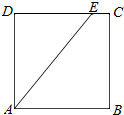 如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.
如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.