题目内容
已知a>0,函数f(x)=x+
(x>0).
(1)试用定义证明:f(x)在(
,+∞)上单调递增;
(2)若x∈[1,3]时,不等式f(x)≥2恒成立,求a的取值范围.
| a |
| a |
(1)试用定义证明:f(x)在(
| a |
(2)若x∈[1,3]时,不等式f(x)≥2恒成立,求a的取值范围.
考点:函数单调性的判断与证明,函数恒成立问题
专题:分类讨论,函数的性质及应用
分析:(1)利用函数单调性的对应证明f(x)在(
,+∞)上的单调性即可;
(Ⅱ)讨论f(x)在(0,+∞)上的单调性,求出f(x)在[1,3]上的最小值f(x)min,使f(x)min≥2,从而求出a的取值范围.
| a |
(Ⅱ)讨论f(x)在(0,+∞)上的单调性,求出f(x)在[1,3]上的最小值f(x)min,使f(x)min≥2,从而求出a的取值范围.
解答:
解:(1)任取x1、x2∈(
,+∞),且x1<x2,
则f(x1)-f(x2)=(x1+
)-(x2+
)=
;┅(2分)
∵
<x1<x2,∴x1x2>0,x1-x2<0,x1x2-a>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2);
∴f(x)在(
,+∞)上单调递增;┅(6分)
(Ⅱ)f(x)在(0,
)上单调递减,在(
,+∞)上单调递增;
①若0<a<1,则f(x)在[1,3]上单调递增,f(x)min=f(1)=1+a;
∴1+a≥2,即a≥1,∴a=1;┅(8分)
②若1<a<9,则f(x)在[1,
]上单调递减,在[
,3]上单调递增,
f(x)min=f(
)=2
;
∴2
≥2,即a≥1,
∴1<a<9;┅(10分)
③若a≥9,则f(x)在[1,3]上单调递减,f(x)min=f(3)=3+
;
∴3+
≥2,即a≥-3,∴a≥9;┅(12分)
综合①②③,a的取值范围是{a|a≥1}.┅(14分)
| a |
则f(x1)-f(x2)=(x1+
| a |
| x1 |
| a |
| x2 |
| (x1-x2)(x1x2-a) |
| x1x2 |
∵
| a |
∴f(x1)-f(x2)<0,
即f(x1)<f(x2);
∴f(x)在(
| a |
(Ⅱ)f(x)在(0,
| a |
| a |
①若0<a<1,则f(x)在[1,3]上单调递增,f(x)min=f(1)=1+a;
∴1+a≥2,即a≥1,∴a=1;┅(8分)
②若1<a<9,则f(x)在[1,
| a |
| a |
f(x)min=f(
| a |
| a |
∴2
| a |
∴1<a<9;┅(10分)
③若a≥9,则f(x)在[1,3]上单调递减,f(x)min=f(3)=3+
| a |
| 3 |
∴3+
| a |
| 3 |
综合①②③,a的取值范围是{a|a≥1}.┅(14分)
点评:本题考查了函数的单调性的证明问题,也考查了分类讨论思想求函数的最值问题,是中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
已知椭圆
+
=1(a>b>0),过焦点F1的弦AB的长是2,另一焦点为F2,则△ABF2的周长是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a | B、4a-2 |
| C、4a | D、4a+4 |
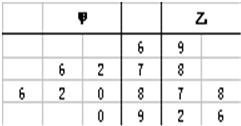 如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )
如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分比乙同学平均分高;
③甲同学成绩的平均分比乙同学平均分低;
④甲同学成绩的方差小于乙同学成绩的方差.
| A、①③ | B、①②④ | C、③④ | D、③ |
给出以下命题:
(1)若
f(x)dx>0,则f(x)>0;
(2)
dx=0;
(3)应用微积分基本定理,有
dx=F(2)-F(1),则F(x)=lnx;
(4)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
f(x)dx=
f(x)dx;
其中正确命题的为( )
(1)若
| ∫ | b a |
(2)
| ∫ | 2π -2π |
| sinx |
| e|x| |
(3)应用微积分基本定理,有
| ∫ | 2 1 |
| 1 |
| x |
(4)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
| ∫ | a 0 |
| ∫ | a+T T |
其中正确命题的为( )
| A、(3),(4) |
| B、(1),(2) |
| C、(1),(4) |
| D、(2),(4) |