题目内容
(本小题满分12分)
设椭圆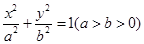 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 满足
满足 .
.
(1)求椭圆的离心率 ;
;
(2)设直线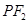 与椭圆相交于A,B两点.若直线
与椭圆相交于A,B两点.若直线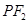 与圆
与圆 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程.
设椭圆
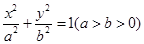 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 满足
满足 .
.(1)求椭圆的离心率
 ;
;(2)设直线
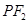 与椭圆相交于A,B两点.若直线
与椭圆相交于A,B两点.若直线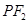 与圆
与圆 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程.解:(1)设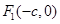 ,
,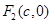 (
(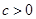 ),因为
),因为 ,
,
所以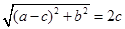 , …………2分
, …………2分
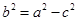 代入,整理得
代入,整理得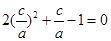 ,
,
即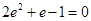 ,解得
,解得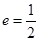 . ……………………5分
. ……………………5分
(2)由(1)知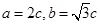 ,可得椭圆方程为
,可得椭圆方程为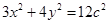 ,
,
直线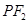 的方程为
的方程为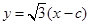 , ……………………7分
, ……………………7分
A,B两点坐标满足方程组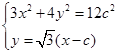 ,消y整理得
,消y整理得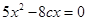 ,
,
解得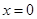 或
或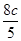 ,所以A,B两点坐标为
,所以A,B两点坐标为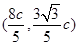 ,
,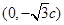 ,
,
所以由两点间距离公式得|AB|=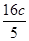 , ……………………9分
, ……………………9分
于是|MN|= |AB|=
|AB|=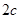 ,圆心
,圆心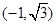 到直线
到直线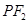 的距离
的距离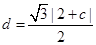 ,
,
因为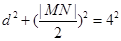 ,所以
,所以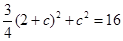 ,解得
,解得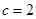 ,
,
所以椭圆方程为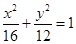 . ……………………12分
. ……………………12分
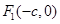 ,
,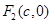 (
(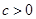 ),因为
),因为 ,
,所以
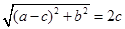 , …………2分
, …………2分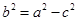 代入,整理得
代入,整理得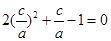 ,
,即
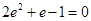 ,解得
,解得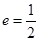 . ……………………5分
. ……………………5分(2)由(1)知
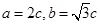 ,可得椭圆方程为
,可得椭圆方程为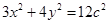 ,
,直线
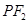 的方程为
的方程为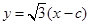 , ……………………7分
, ……………………7分A,B两点坐标满足方程组
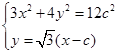 ,消y整理得
,消y整理得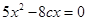 ,
,解得
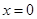 或
或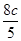 ,所以A,B两点坐标为
,所以A,B两点坐标为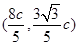 ,
,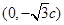 ,
, 所以由两点间距离公式得|AB|=
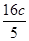 , ……………………9分
, ……………………9分于是|MN|=
 |AB|=
|AB|=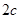 ,圆心
,圆心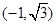 到直线
到直线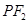 的距离
的距离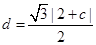 ,
,因为
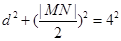 ,所以
,所以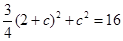 ,解得
,解得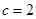 ,
,所以椭圆方程为
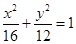 . ……………………12分
. ……………………12分略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
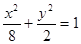 经过点
经过点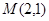 ,
,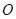 为坐标原点,平行于
为坐标原点,平行于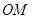 的直线
的直线 在
在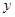 轴上的截距为
轴上的截距为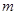
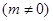 .
.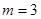 时,判断直线
时,判断直线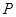 为椭圆上的动点,求点
为椭圆上的动点,求点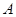 、
、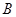 两个不同点时,求证:直线
两个不同点时,求证:直线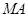 、
、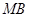 与
与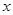 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.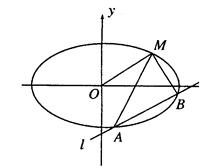
 +
+ =1的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )
=1的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )


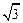 ,求△AOB面积的最大值.
,求△AOB面积的最大值.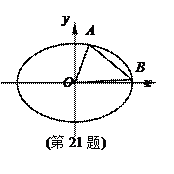
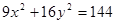 内有一点P
内有一点P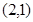 ,以P为中点作弦MN,则直线MN的方程是( )
,以P为中点作弦MN,则直线MN的方程是( )



 的离心率为( )
的离心率为( )


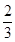
 ,且长轴长是短轴长的2倍,则该椭圆的标准方程是________.
,且长轴长是短轴长的2倍,则该椭圆的标准方程是________.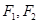 分别为椭圆
分别为椭圆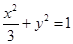 的焦点,点
的焦点,点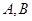 在椭圆上,若
在椭圆上,若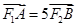 ;则点
;则点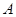
 的坐标是 _________
的坐标是 _________