Question

4．定义某种运算S=a?b，运算原理如图所示，则式子[（2tan$\frac{13π}{4}$）?lg$\frac{1}{10}$]+[lne?（$\frac{1}{5}$）^-1]的值为（　　）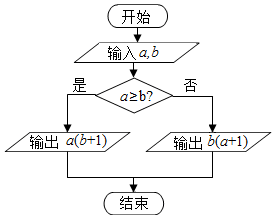

• A． 4
• B． 8
• C． 10
• D． 13

Answer 1

分析 根据程序框图可得，当a≥b时，则输出a（b+1），反之，则输出b（a+1），比较2tan$\frac{13π}{4}$与lg$\frac{1}{10}$，lne与（$\frac{1}{5}$）^-1的大小，即可求解得到答案．

解答 解：模拟执行程序，可得，当a≥b时，则输出a（b+1），反之，则输出b（a+1），
∵2tan$\frac{13π}{4}$=2，lg$\frac{1}{10}$=-1，
∴（2tan$\frac{13π}{4}$）?lg$\frac{1}{10}$=（2tan$\frac{13π}{4}$）×（lg$\frac{1}{10}$+1）=2×（-1+1）=0，
∵lne=1，（$\frac{1}{5}$）^-1=5，
∴lne?（$\frac{1}{5}$）^-1=（$\frac{1}{5}$）^-1×（lne+1）=5×（1+1）=10，
∴[（2tan$\frac{13π}{4}$）?lg$\frac{1}{10}$]+[lne?（$\frac{1}{5}$）^-1]=0+10=10．
故选：C．

点评 本题考查了程序框图，对应的知识点是条件结构的应用，其中正确理解各变量的含义并根据程序功能的需要合理的分析是解答的关键．属于基础题．