题目内容
13．已知p：（x+1）（x-3）＜0，q：3x-4＜m，若p是q的充分不必要条件，则实数m的取值范围是[5，+∞）．分析 分别化简命题p，q，利用p是q的充分不必要条件即可得出．
解答 解：p：（x+1）（x-3）＜0，解得-1＜x＜3．
q：3x-4＜m，解得x$＜\frac{1}{3}（4+m）$．
∵p是q的充分不必要条件，
∴$3≤\frac{1}{3}（4+m）$，解得m≥5．
则实数m的取值范围是[5，+∞）．
故答案为：[5，+∞）．
点评 本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
4．定义某种运算S=a?b，运算原理如图所示，则式子[（2tan$\frac{13π}{4}$）?lg$\frac{1}{10}$]+[lne?（$\frac{1}{5}$）-1]的值为（ ）
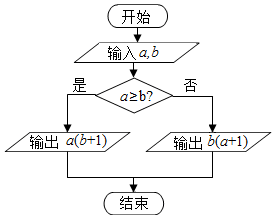
| A． | 4 | B． | 8 | C． | 10 | D． | 13 |
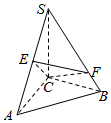直线SC⊥面ABC，AB⊥BC，且AB=BC=1，SA=2，E为SA中点，F为点C在线BS上的射影．