题目内容
16.已知△ABC的三内角A,B,C依次构成等差数列,则cosA+cosC的取值范围为($\frac{1}{2}$,1].分析 根据题意求出B=$\frac{π}{3}$,再用A表示出C,利用两角和与差的余弦公式即可求出cosA+cosC的取值范围.
解答 解:∵△ABC的三内角A,B,C成等差数列,
∴2B=A+C,
又A+B+C=π,
∴3B=π,即B=$\frac{π}{3}$;
∴C=$\frac{2π}{3}$-A,A∈(0,$\frac{2π}{3}$),
∴cosA+cosC=cosA+cos($\frac{2π}{3}$-A)
=cosA+(-$\frac{1}{2}$cosA+$\frac{\sqrt{3}}{2}$sinA)
=$\frac{1}{2}$cosA+$\frac{\sqrt{3}}{2}$sinA
=cos(A-$\frac{π}{3}$);
由A∈(0,$\frac{2π}{3}$),得A-$\frac{π}{3}$∈(-$\frac{π}{3}$,$\frac{π}{3}$),
∴cos(A-$\frac{π}{3}$)∈($\frac{1}{2}$,1];
即cosA+cosC的取值范围是($\frac{1}{2}$,1].
故答案为:($\frac{1}{2}$,1].
点评 本题考查了三角函数的取值范围问题,把问题转化为关于角A的三角函数是解决问题的关键,属中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
4.定义某种运算S=a?b,运算原理如图所示,则式子[(2tan$\frac{13π}{4}$)?lg$\frac{1}{10}$]+[lne?($\frac{1}{5}$)-1]的值为( )
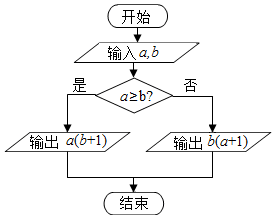

| A. | 4 | B. | 8 | C. | 10 | D. | 13 |
11.若sin2α<0且tanαcosα>0,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |