题目内容
16.命题“?x>0,都有x≥1”的否定为?x>0,使得x<1.分析 利用全称命题的否定是特称命题,去判断.
解答 解:因为命题是全称命题,根据全称命题的否定是特称命题,
所以命题的否定:?x>0,使得x<1.
故答案为:?x>0,使得x<1
点评 本题主要考查全称命题的否定,要求掌握全称命题的否定是特称命题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
4.已知m,n是两条不同直线,α,β是两个不同的平面,且n?β,则下列叙述正确的是( )
| A. | 若m∥n,m?α,则α∥β | B. | 若α∥β,m?α,则m∥n | C. | 若α∥β,m⊥n,则m⊥α | D. | 若m∥n,m⊥α,则α⊥β |
11.已知抛物线x=4y2上一点P(m,1),焦点为F.则|PF|=( )
| A. | m+1 | B. | 2 | C. | $\frac{63}{16}$ | D. | $\frac{65}{16}$ |
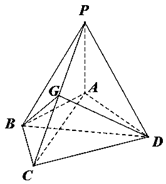 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,∠ABC=120°,G为线段PC上的点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,∠ABC=120°,G为线段PC上的点.