题目内容
11.已知△ABC中,BC=2,AC=2AB,则△ABC面积的最大值为$\frac{4}{3}$.分析 设AB=x,则AC=2x,根据面积公式得S△ABC=$\sqrt{1-co{s}^{2}B}$x,由余弦定理求得 cosC代入化简 S△ABC=$\sqrt{\frac{16}{9}-\frac{9({x}^{2}-\frac{20}{9})^{2}}{16}}$,由三角形三边关系求得$\frac{2}{3}$<x<2,由二次函数的性质求得S△ABC取得最大值.
解答 解:依题意,设AB=x,则AC=2x,又BC=2,
根据面积公式得S△ABC=$\frac{1}{2}$AB•BC•sinB=sinBx=$\sqrt{1-co{s}^{2}B}$x.
由余弦定理得:cosB=$\frac{{x}^{2}+{2}^{2}-(2x)^{2}}{2×2×x}$=$\frac{4-3{x}^{2}}{4x}$,
∴S△ABC=$\sqrt{1-co{s}^{2}B}$x=$\sqrt{1-(\frac{4-3{x}^{2}}{4x})^{2}}$x=$\sqrt{\frac{16}{9}-\frac{9({x}^{2}-\frac{20}{9})^{2}}{16}}$
由三角形三边关系有:x+2x>2且x+2>2x,解得:$\frac{2}{3}$<x<2,
故当 x=$\frac{2\sqrt{5}}{3}$时,S△ABC取得最大值$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题主要考查了余弦定理和面积公式在解三角形中的应用.当涉及最值问题时,可考虑用函数的单调性和定义域等问题,考查了转化思想,属于中档题.

练习册系列答案
相关题目
19.已知动直线l0:ax+by+c-2=0(a>0,c>0)恒过点P(1,m)且Q(4,0)到动直线l0的最大距离为3,则$\frac{1}{2a}$+$\frac{2}{c}$的最小值为( )
| A. | $\frac{9}{2}$ | B. | $\frac{9}{4}$ | C. | 1 | D. | 9 |
16.若sin(π-α)=$\frac{1}{3}$,且$\frac{π}{2}$≤α≤π,则sin2α的值为( )
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | -$\frac{2\sqrt{2}}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |
3.已知集合A={x|x2-2x-3>0},B={x|lg(x-2)≤1},则(∁RA)∪B=( )
| A. | (-1,12) | B. | (2,3) | C. | (2,3] | D. | [-1,12] |
1.已知z=ai(a∈R),(1+z)(1+i)是实数,则|z+2|=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
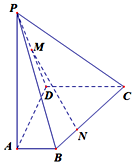 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$. 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有42株树木的底部周长小于110cm.
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有42株树木的底部周长小于110cm.