Question

16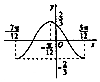．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的部分图象如图所示，则f（$\frac{π}{12}$）=（　　）

• A． $\frac{1}{3}$
• B． $\frac{\sqrt{2}}{3}$
• C． $\frac{\sqrt{3}}{3}$
• D． $\frac{2}{3}$

Answer 1

分析 根据函数的最高点和最低点可得A的值，根据图象T=$\frac{5π}{12}-（-\frac{7π}{12}）$=π，可得ω，图象过（$-\frac{7π}{12}$，-$\frac{2}{3}$）带入求解φ，可函数f（x）的解析式．可得f（$\frac{π}{12}$）的值．

解答 解：由图象知最高点为$\frac{2}{3}$，最低点为$-\frac{2}{3}$，∴A=$\frac{2}{3}$
根据图象T=$\frac{5π}{12}-（-\frac{7π}{12}）$=π，∴ω=$\frac{2π}{T}$=2．
∵图象过（$-\frac{π}{12}$，$\frac{2}{3}$）带入可得：$\frac{2}{3}=\frac{2}{3}sin（-2×\frac{π}{12}+φ）$，
得：φ-$\frac{π}{6}$=$\frac{π}{2}$+2kπ，（k∈Z）
φ=$\frac{2π}{3}+2kπ$，（k∈Z）
那么：函数f（x）=$\frac{2}{3}$sin（2x$+\frac{2π}{3}$+2kπ）=$\frac{2}{3}$sin（2x$+\frac{2π}{3}$）
当x=$\frac{π}{12}$时，即f（$\frac{π}{12}$）=$\frac{2}{3}$sin（2×$\frac{π}{12}$$+\frac{2π}{3}$）=$\frac{1}{3}$
故选A．

点评 本题主要考查三角函数的图象和性质，根据图象求出函数的解析式是解决本题的关键．要求熟练掌握函数图象之间的变化关系．