题目内容
4.若锐角α,β满足$tanα+tanβ=\sqrt{3}-\sqrt{3}tanαtanβ$,则α+β=$\frac{π}{3}$.分析 由题意和两角和的正切函数求出tan(α+β),由α和β的范围求出α+β的范围,由特殊角的三角函数值求出α+β的值.
解答 解:∵$tanα+tanβ=\sqrt{3}-\sqrt{3}tanαtanβ$,
∴$tan(α+β)=\frac{tanα+tanβ}{1-tanαtanβ}$=$\sqrt{3}$,
∵α、β是锐角,∴0<α+β<π,
则α+β=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题考查两角和的正切函数,注意角的范围,属于基础题.

练习册系列答案
相关题目
16.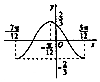 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
15.已知命题p:抛物线方程是x=4y2,则它的准线方程为x=1,命题q:双曲线$\frac{x^2}{4}-\frac{y^2}{5}=-1$的一个焦点是(0,3),其中真命题是( )
| A. | p | B. | ¬q | C. | p∧q | D. | p∨q |
16.已知命题p:|x-4|≤6,q:x2-m2-2x+1≤0(m>0),若¬p是¬q的必要不充分条件,则实数m的取值范围为( )
| A. | [9,13] | B. | (3,9) | C. | [9,+∞) | D. | (9,+∞) |
13.设x,y满足约束条件$\left\{\begin{array}{l}y-x≤0\\ x+2y≤4\\ x-2y≤2\end{array}\right.$,则z=x-3y的最大值为( )
| A. | 4 | B. | $\frac{3}{2}$ | C. | $-\frac{8}{3}$ | D. | 2 |
14.函数f(x)=(x-1)2的单调递增区间是( )
| A. | [0,+∞) | B. | [1,+∞) | C. | (-∞,0] | D. | (-∞,1] |