题目内容
10.若x,y>0,则$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$的最大值为$\sqrt{2}$.分析 利用基本不等式即可求出.
解答 解:∵x,y>0,
∴x+y≥2$\sqrt{xy}$,当且仅当x=y时取等号,
($\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$)2=$\frac{x+y+2\sqrt{xy}}{x+y}$=1+$\frac{2\sqrt{xy}}{x+y}$≤1+1=2,
∴$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$≤$\sqrt{2}$,
故最大值为$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查了基本不等式的应用,关键是灵活变形,属于基础题.

练习册系列答案
相关题目
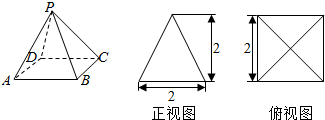 四棱锥P-ABCD及其正(主)视图和俯视图如图所示.
四棱锥P-ABCD及其正(主)视图和俯视图如图所示.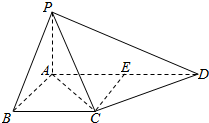 如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.