题目内容
某工厂用两种不同的原料均可生产同一产品,若采用甲种原料,每吨成本1000元,运费500元,可生产产品90千克,乙采用一种原料,每吨成本1500元,运费400元,可生产产品100千克,若每日预算总成本不得超过6500元,运费不得超过2200元,问此工厂如何安排每日可生产产品最多?最多生产多少千克?
考点:简单线性规划的应用
专题:不等式的解法及应用
分析:设采用甲种原料x吨,乙种原料y吨,建立目标函数和约束条件,利用线性规划进行求解即可.
解答:
解:设采用甲种原料x吨,乙种原料y吨.生产产品z千克,
依题意可得线性约束条件
,即
,
目标函数为z=90x+100y,
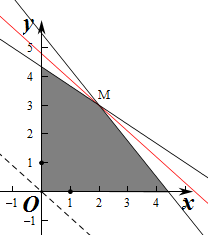
作出线性约束条件所表示的平面区域如图所示
将z=90x+100y变形为y=-
x+
,
当直线y=-
x+
在纵轴上的截距达到最大值时,
即直线y=-
x+
经过点M时,z也达到最大值.
由
得
,M点的坐标为(2,3),
所以当x=2,y=3时,zmax=90×2+100×3=480.
依题意可得线性约束条件
|
|
目标函数为z=90x+100y,
作出线性约束条件所表示的平面区域如图所示
将z=90x+100y变形为y=-
| 9 |
| 10 |
| z |
| 100 |

当直线y=-
| 9 |
| 10 |
| z |
| 100 |
即直线y=-
| 9 |
| 10 |
| z |
| 100 |
由
|
|
所以当x=2,y=3时,zmax=90×2+100×3=480.
点评:本题主要考查线性规划的应用问题,根据条件建立约束条件,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
函数f(x)=Asin(2x+φ)(A,φ∈R)的部分图象如图所示,那么f(
)=( )

| π |
| 6 |

| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,把函数g(x)=f(x)-x的零点按照从大到小的顺序排成一个数列{an}
,则该数列的通项公式为( )
|
,则该数列的通项公式为( )
| A、an=n-1(n∈N*) |
| B、an=n(n∈N*) |
| C、an=n(n-1)(n∈N*) |
| D、an=2n-2(n∈N*) |
已知x∈R,则“x2-3x≤0”是“(x-1)(x-2)≤0成立”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
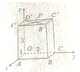 如图所示,在长方形OABC-D′A′B′C′中,|OA|=1,|OC|=2,|OD′|=3,A′C′与B′D′交于点P,分别写出点C,C′,B,B′,A′,A,P的坐标.
如图所示,在长方形OABC-D′A′B′C′中,|OA|=1,|OC|=2,|OD′|=3,A′C′与B′D′交于点P,分别写出点C,C′,B,B′,A′,A,P的坐标.