题目内容
已知数列{an}满足a1=1,a2=2,an+2=(1+cos2
)•an+sin2
(n∈N*),则该数列{an}的前n项和为 .
| nπ |
| 2 |
| nπ |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:先利用题中条件找到数列的特点,即其奇数项构成了首项为1,公差为1的等差数列,而其偶数项则构成了首项为2,公比为2的等比数列,再对其和用分组求和的方法找到即可.
解答:
解:由题中条件知,a1=1,a2=2,a3=a1+1=2,a4=2a2+0=4,a5=a3+1=3,a6=2a4=8…
即其奇数项构成了首项为1,公差为1的等差数列,而其偶数项则构成了首项为2,公比为2的等比数列,
∴当n为奇数时,sn=
×1+
×1+
=
+2
-2,
当n为偶数时,sn=
×1+
×1+
=
+2
-2.
∴sn=
.
故答案为:sn=
.
即其奇数项构成了首项为1,公差为1的等差数列,而其偶数项则构成了首项为2,公比为2的等比数列,
∴当n为奇数时,sn=
| n+1 |
| 2 |
| ||||
| 2 |
2(1-2
| ||
| 1-2 |
| (n+1)(n+3) |
| 8 |
| n+1 |
| 2 |
当n为偶数时,sn=
| n |
| 2 |
| ||||
| 2 |
2(1-2
| ||
| 1-2 |
| n(n+2) |
| 8 |
| n+2 |
| 2 |
∴sn=
|
故答案为:sn=
|
点评:本题主要考查等差数列和等比数列的前n项和公式.考查学生的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
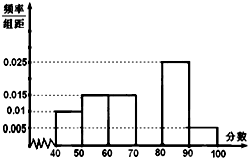 某校从参加高一年级期末考试的学生中抽出20名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100],然后画出如下所示频率分布直方图,但是缺失了第四组[70,80)的信息.观察图形的信息,回答下列问题.
某校从参加高一年级期末考试的学生中抽出20名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100],然后画出如下所示频率分布直方图,但是缺失了第四组[70,80)的信息.观察图形的信息,回答下列问题. 已知某几何体的三视图如图所示,其中正视图是直角三角形,侧视图是正三角形,俯视图是边长为2的正方形,则此几何体的表面积为
已知某几何体的三视图如图所示,其中正视图是直角三角形,侧视图是正三角形,俯视图是边长为2的正方形,则此几何体的表面积为