题目内容
10．已知函数f（x）=$\sqrt{2-ax}$在区间[0，2]上单调递减，则a的取值范围是（0，1]．分析 由题意利用函数的单调性的性质可得可得$\left\{\begin{array}{l}{-a＜0}\\{2-2a≥0}\end{array}\right.$，由此求得a的范围．
解答 解：根据函数f（x）=$\sqrt{2-ax}$在区间[0，2]上单调递减，可得$\left\{\begin{array}{l}{-a＜0}\\{2-2a≥0}\end{array}\right.$，
求得0＜a≤1，
故答案为：（0，1]．
点评 本题主要考查函数的单调性的性质，函数的定义域，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图是用条件语句编写的一个程序：若输入4，则输出的结果是15，该程序的功能是求函数$y=\left\{{\begin{array}{l}{{x^2}-1}\\ 2\\{2x}\end{array}}\right.，\begin{array}{l}{x＞3}\\{x=3}\\{x＜3}\end{array}$的值．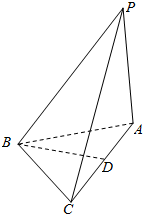
如图，三棱锥P-ABC中，PA⊥平面ABC，AB=BC，AC=2$\sqrt{2}$，PA=2，D是AC的中点