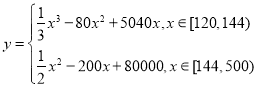题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1) 见解析.
(2)证明见解析.
【解析】分析:(1)先求导数,再根据二次方程![]() =0根得情况分类讨论:当
=0根得情况分类讨论:当![]() 时,
时,![]() .∴
.∴![]() 在
在![]() 上单调递减. 当
上单调递减. 当![]() 时,根据两根大小再分类讨论对应单调区间, (2)先化简不等式
时,根据两根大小再分类讨论对应单调区间, (2)先化简不等式![]() 消m得
消m得![]() ,再利用导数研究
,再利用导数研究![]() ,
,![]() 单调性,得其最小值大于-1,即证得结果.
单调性,得其最小值大于-1,即证得结果.
详解:(1)由![]() ,得
,得
![]()
![]() ,
,![]() .
.
设![]() ,
,![]() .
.
当![]() 时,即
时,即![]() 时,
时,![]() ,
,![]() .
.
∴![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,即
时,即![]() 时,
时,
令![]() ,得
,得![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,
在![]() 上,
上,![]() ,在
,在![]() 上,
上,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)∵![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,
,
∴由(1)知![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,
,
![]() ,
,![]() ,且
,且![]() ,此时,
,此时,![]() ,
,
要证明![]() ,只要证明
,只要证明![]() .
.
∵![]() ,∴只要证明
,∴只要证明![]() 成立.
成立.
∵![]() ,∴
,∴![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,
,
∴![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() 时,
时,![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目