题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知![]() ,记
,记![]() (
(![]() 且
且![]() ),是否存在这样的常数
),是否存在这样的常数![]() ,使得数列
,使得数列![]() 是常数列,若存在,求出
是常数列,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若数列![]() ,对于任意的正整数
,对于任意的正整数![]() ,均有
,均有 成立,求证:数列
成立,求证:数列![]() 是等差数列.
是等差数列.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)根据和项与通项关系得![]() ,再根据等比数列定义与通项公式求解(2)先化简
,再根据等比数列定义与通项公式求解(2)先化简![]() ,再根据恒成立思想求
,再根据恒成立思想求![]() 的值(3)根据和项得
的值(3)根据和项得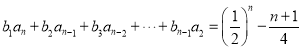 ,再作差得
,再作差得![]() ,最后根据等差数列定义证明.
,最后根据等差数列定义证明.
(1)![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() 时,
时,![]() ,
,
两式相减得,![]() ,
,![]() ,
,
数列![]() 是以2为首项,公比为
是以2为首项,公比为![]() 的等比数列,所以
的等比数列,所以![]() .
.
(2)若数列![]() 是常数列,
是常数列,
![]()
![]() 为常数.
为常数.
只有![]() ,解得
,解得![]() ,
,
此时![]() .
.
(3)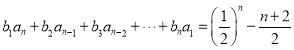 ①
①
![]() ,
,![]() ,其中
,其中![]() ,所以
,所以![]() ,
,
当![]() 时,
时,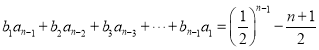 ②
②
②式两边同时乘以![]() 得,
得,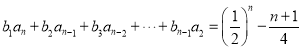 ③
③
①式减去③得,![]() ,所以
,所以![]() ,
,
因为![]() ,
,
所以数列![]() 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列.
的等差数列.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目