题目内容
抛物线y=x2上的一动点M到直线l:x-y-1=0距离的最小值是 .
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设抛物线上的任意一点M(m,m2),由点到直线的距离公司可求M到直线x-y-1=0的距离,由二次函数的性质可求M到直线x-y-1=0的最小距离.
解答:
解:设抛物线上的任意一点M(m,m2)
M到直线x-y-1=0的距离d=
=
由二次函数的性质可知,当m=
时,最小距离d=
.
故答案为:
.
M到直线x-y-1=0的距离d=
| |m-m2-1| | ||
|
|(m-
| ||||
|
由二次函数的性质可知,当m=
| 1 |
| 2 |
3
| ||
| 8 |
故答案为:
3
| ||
| 8 |
点评:本题考查直线与抛物线的位置关系的应用,解题时要注意公式的灵活运用,抛物线的基本性质和点到线的距离公式的应用,考查综合运用能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
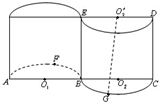 如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为 在一个盒子中有分别标有数字0,1,2,3,4的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之和为偶数的概率是
在一个盒子中有分别标有数字0,1,2,3,4的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之和为偶数的概率是