题目内容
已知A、B、C是单位圆上三个互不相同的点,若|
|=|
|,则
•
的最小值是 .
| AB |
| AC |
| AB |
| AC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,取
=(1,0),不妨设B(cosθ,sinθ),(θ∈(0,π)).由于|
|=|
|,可得C(cosθ,-sinθ).再利用数量积运算、二次函数的单调性、余弦函数的单调性即可得出.
| OA |
| AB |
| AC |
解答:
解:如图所示,取
=(1,0),不妨设B(cosθ,sinθ),(θ∈(0,π)).
∵|
|=|
|,∴C(cosθ,-sinθ).
∴
•
=(cosθ-1,sinθ)•(cosθ-1,-sinθ)
=(cosθ-1)2-sin2θ
=2(cosθ-
)2-
,
当且仅当cosθ=
,即θ=
时,上式取得最小值-
.
即
•
的最小值是-
.
故答案为:-
.
| OA |

∵|
| AB |
| AC |
∴
| AB |
| AC |
=(cosθ-1)2-sin2θ
=2(cosθ-
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当cosθ=
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
即
| AB |
| AC |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了数量积运算、二次函数的单调性、余弦函数的单调性,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
设△ABC的面积为S,已知S=a2-(b-c)2,则tan
的值为( )
| A |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
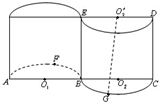 如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为 在一个盒子中有分别标有数字0,1,2,3,4的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之和为偶数的概率是
在一个盒子中有分别标有数字0,1,2,3,4的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之和为偶数的概率是