题目内容
函数f(x)=x(1-x)的单调增区间为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据函数f(x)=-(x-
)2+
,可得函数的增区间.
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:由于函数f(x)=x(1-x)=-(x-
)2+
,故函数的增区间为(-∞,
],
故答案为:(-∞,
].
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
故答案为:(-∞,
| 1 |
| 2 |
点评:本题主要考查二次函数的单调性,属于基础题.

练习册系列答案
相关题目
已知点M(x,y)为平面区域
内的一个动点,则
的最小值为( )
|
| (x+1)2+y2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
下列各图表示两个变量x、y的对应关系,则下列判断正确的是( )
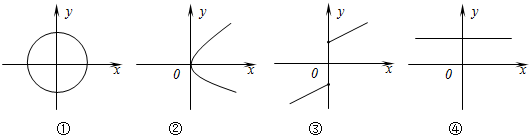

| A、都表示映射,都表示y是x的函数 |
| B、仅③表示y是x的函数 |
| C、仅④表示y是x的函数 |
| D、都不能表示y是x的函数 |
函数y=cos2(x-
)-cos2(x+
)是( )
| π |
| 4 |
| π |
| 4 |
| A、最小正周期为π的奇函数 | ||
| B、最小正周期为π的偶函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|