题目内容
已α、β都是锐角,且sinα=
,sinβ=
,求证:α+β=
.
| ||
| 5 |
| ||
| 10 |
| π |
| 4 |
证明:∵α、β都是锐角,sinα=
,sinβ=
,
∴cosα=
=
,cosβ=
=
,
则cos(α+β)=cosαcosβ-sinαsinβ
=
×
-
×
=
,
又α+β∈(0,π),
∴α+β=
.
| ||
| 5 |
| ||
| 10 |
∴cosα=
| 1-sin2α |
2
| ||
| 5 |
| 1-sin2β |
3
| ||
| 10 |
则cos(α+β)=cosαcosβ-sinαsinβ
=
2
| ||
| 5 |
3
| ||
| 10 |
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
又α+β∈(0,π),
∴α+β=
| π |
| 4 |

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
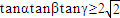 .
.