题目内容
(1)已知α、β、γ都是锐角,且tanα=(2)求arctan1+arctan2+arctan3的值.
思路分析:对于第(1)小题可先求出tan(α+β)的值,再把α+β视为一个整体,求出tan[(α+β)+γ]的值,最后用反正切函数表示出α+β+γ的值;对于第(2)小题,由于arctan1=π[]4,所以只需求出arctan2+arctan3的值即可.
解:(1)∵tanα=![]() ,tanβ=
,tanβ=![]() ,∴
,∴ .
.
又∵tanγ=![]() ,
,
∴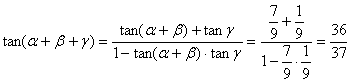 .
.
∵α是锐角,且![]() ,∴0<α<
,∴0<α<![]() .
.
同理,可得0<β<![]() ,0<γ<
,0<γ<![]() .
.
∴0<α+β+γ<![]() .
.
∴α+β+γ=arctan![]() .
.
(2)设arctan2=α,arctan3=β,
则tanα=2,tanβ=3且![]() <α<
<α<![]() ,
,![]() <β<
<β<![]() .
.
∵![]() ,
,
又![]() <α+β<π,∴α+β=
<α+β<π,∴α+β=![]() ,
,
即arctan2+arctan3=![]() .
.
又arctan1=![]() ,∴arctan1+arctan2+arctan3=π.
,∴arctan1+arctan2+arctan3=π.
方法归纳 已知三角函数值求角,需界定角的范围,为准确地求出所求的角,可根据三角函数的单调性,把所求的角放置于两个特殊角之间,以进一步缩小所求角的范围,避免增根的出现.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目