题目内容
已知α、β、γ都是锐角,且cos2α+cos2β+cos2γ=1,求证:tanαtanβtanγ≥2| 2 |
分析:α、β、γ都是锐角,可以看做长方体的一条对角线(长为1)与相邻3个面的夹角,
用长方体的一顶点上3条棱abc表示tanα、tanβ、tanγ,再用均值不等式a2+b2≥2ab.
用长方体的一顶点上3条棱abc表示tanα、tanβ、tanγ,再用均值不等式a2+b2≥2ab.
解答:解:通过观察、联想:在长方体中,a2+b2+c2=l2?(
)2+(
)2+(
)2=1
∵α、β、γ是锐角,∴令
=cosα,
=cosβ,
=cosγ
∴tanα=
≥
,tanβ≥
,tanγ≥
,
∴tanαtanβtanγ≥2
.
| a |
| l |
| b |
| l |
| c |
| l |
∵α、β、γ是锐角,∴令
| a |
| l |
| b |
| l |
| c |
| l |
∴tanα=
| ||
| a |
| ||||
| a |
| ||||
| b |
| ||||
| c |
∴tanαtanβtanγ≥2
| 2 |
点评:本题体现了划归转化的数学思想方法,注意均值不等式a2+b2≥2ab的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
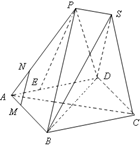 已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
 已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、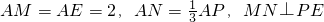 .
.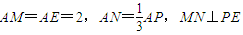 .
.
 .
.