��Ŀ����
10��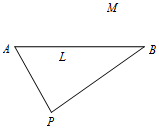 �ұ߷��ֽӵ��鱨���ں���AB����ֱ��l��һ���M������˽�Ż��ڽ��н�����߷���Ѹ���ɳ���ͧǰȥ�Ѳ�����ͼ����֪��ͧ����λ����l����һ����ͷP����PA=8���PB=10�����APB=60�㣮
�ұ߷��ֽӵ��鱨���ں���AB����ֱ��l��һ���M������˽�Ż��ڽ��н�����߷���Ѹ���ɳ���ͧǰȥ�Ѳ�����ͼ����֪��ͧ����λ����l����һ����ͷP����PA=8���PB=10�����APB=60�㣮��1���Ƿ���ڵ�M��ʹ��ͧ�غ���P��A��M��P��B��M��·����ȣ�����ڣ������ʵ���ֱ������ϵ�������M�Ĺ켣���̣��һ����켣�Ĵ���ͼ�Σ��粻���ڣ���˵�����ɣ�
��2������˽����������������ʱ��·��P��A��M��·��P��B��M��·�̶̣���˵�����ɣ�
���� ��1����������ϵ������˫���ߵĶ��壬�ɵý��ۣ�
��2����˽����ֱ��l����࣬���ڣ�1�������ߵ���������ʱ��·��P��A��M��̣�
��� �⣺��1��������ͼ��ʾ������ϵ��|MA|-|MB|=2��
��M�Ĺ켣��˫���ߵ���֧��|AB|=$\sqrt{64+100-80}$=2$\sqrt{21}$��
��$a=1��c=\sqrt{21}��{b}^{2}=20$��
��M�Ĺ켣������${x}^{2}-\frac{{y}^{2}}{20}$=1��x��1��y��0����
��2����˽����ֱ��l����࣬���ڣ�1�������ߵ���������ʱ��·��P��A��M��̣�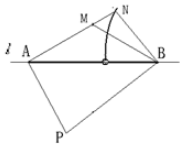
���ɣ���AM���ӳ����루1�������߽��ڵ�N����PA+AN=PB+BN��
PA+AM=PA+AN-MN=PB+BN-MN��PB+BM��
���� ���⿼��������ѧ֪ʶ���ʵ�����⣬����˫���ߵĶ����뷽�̣������е��⣮

��ϰ��ϵ�д�
�����Ŀ
7����֪����y=f��x����x=5�������߷�����y=-x+5����f��5����f'��5���ֱ�Ϊ��������
| A�� | 3��3 | B�� | 3��-1 | C�� | -1��3 | D�� | 0��-1 |
1����֪ʵ��a��0������$f��x��=\left\{\begin{array}{l}{x^2}+2a��\;x��1\\-x��x��1\end{array}\right.$����f��1-a����f��1+a������ʵ��a��ȡֵ��Χ�ǣ�������
| A�� | ��-�ޣ�-2] | B�� | [-2��-1] | C�� | [-1��0�� | D�� | ��-�ޣ�0�� |
18����6����ͬ����ѧ�������ͬһ������ϣ���ͬ�ķŷ��У�������
| A�� | 6 | B�� | 24 | C�� | 120 | D�� | 720 |
2�����в���ʽ��ȷ���ǣ�������
| A�� | a3��a2��a��0����a��1�� | B�� | 0.30.8��0.30.7 | C�� | ��-1��e-1 | D�� | log34��log43 |
19���躯��f��x����x=1�����ڵ�������$\lim_{��x��0}\frac{f��1+��x��-f��1��}{3��x}$=��������
| A�� | $\frac{1}{3}f'��1��$ | B�� | 3f'��1�� | C�� | f'��1�� | D�� | f'��3�� |