题目内容
16.若直线ax+by=1(a,b都是正实数)与圆x2+y2=1相交于A,B两点,当△AOB(O是坐标原点)的面积为$\frac{1}{2}$,a+b的最大值为2.分析 利用△AOB(O是坐标原点)的面积为$\frac{1}{2}$,求出OA⊥OB,可得圆心到直线的距离d=$\frac{1}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{2}}{2}$,即a2+b2=2,利用(a+b)2≤2(a2+b2)=4,即可得出结论.
解答 解:由题意,△AOB(O是坐标原点)的面积为$\frac{1}{2}×1×1×sin∠AOB$=$\frac{1}{2}$,∴sin∠AOB=1,
∴∠AOB=90°,∴OA⊥OB,
∴圆心到直线的距离d=$\frac{1}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{2}}{2}$,∴a2+b2=2,
∴(a+b)2≤2(a2+b2)=4,
∴a+b≤2,即a+b的最大值为2.
故答案为:2.
点评 本题考查直线与圆的位置关系,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.抛物线y2=4x的焦点到双曲线x2-$\frac{{y}^{2}}{2}$=1的渐近线的距离等于( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
7.已知区间U={1,2,3,4,5},A={1,2,3},B={1,4},则(∁UA)∩B=( )
| A. | {4} | B. | {1} | C. | {4,5} | D. | {1,4,5} |
4. 下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )
下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )
 下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )
下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )| A. | 230.5,220 | B. | 231.5,232 | C. | 231,231 | D. | 232,231 |
11.在△ABC中,|AB|=5,|AC|=6,若B=2C,则边BC的长为( )
| A. | 5 | B. | $\frac{11}{5}$ | C. | $\frac{9}{5}$ | D. | $\frac{7}{5}$ |
5.点M(3,2)到拋物线C:y=ax2(a>0)准线的距离为4,F为拋物线的焦点,点N(l,l),当点P在直线l:x-y=2上运动时,$\frac{|PN|-1}{|PF|}$的最小值为( )
| A. | $\frac{3-2\sqrt{2}}{8}$ | B. | $\frac{2-\sqrt{2}}{4}$ | C. | $\frac{5-2\sqrt{2}}{8}$ | D. | $\frac{5-2\sqrt{2}}{4}$ |
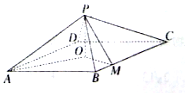 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面$ABCD,AB=2,∠BAD=\frac{π}{3},M$为BC上一点,且$BM=\frac{1}{2}$.
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面$ABCD,AB=2,∠BAD=\frac{π}{3},M$为BC上一点,且$BM=\frac{1}{2}$.