题目内容
16.等比数列{an}的前n项和为Sn,若a3=$\frac{3}{2}$,S3=$\frac{9}{2}$求a1与q.分析 由题意可知当q≠1时,$\left\{\begin{array}{l}{{a}_{1}•{q}^{2}={a}_{3}}\\{\frac{{a}_{1}-{a}_{3}q}{1-q}={S}_{3}}\end{array}\right.$,代入即可求得a1和q的值,当q=1时,则a1=a3=$\frac{3}{2}$,S3=3a1=$\frac{9}{2}$,满足,故当q=1时,成立,即可求得a1与q.
解答 解:由题意可知:等比数列{an}首项为a1,公比为q,
由题意可知:当q≠1时,$\left\{\begin{array}{l}{{a}_{1}•{q}^{2}={a}_{3}}\\{\frac{{a}_{1}-{a}_{3}q}{1-q}={S}_{3}}\end{array}\right.$,即$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=\frac{3}{2}}\\{\frac{{a}_{1}-\frac{3}{2}q}{1-q}=\frac{9}{2}}\end{array}\right.$,
整理得:2q3-3q2+1=0,即(q-1)2(2q+1)=0,
解得:q=1(舍去)或q=-$\frac{1}{2}$,
∴当q=-$\frac{1}{2}$,解得:a1=6,
当q=1时,则a1=a3=$\frac{3}{2}$,S3=3a1=$\frac{9}{2}$,满足,故当q=1时,成立,
∴a1=$\frac{3}{2}$,q=1,或q=-$\frac{1}{2}$,a1=6.
点评 本题考查等比数列的前n项和公式的应用,考查分类讨论思想,考查计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.已知直线y=x+a与曲线$y=\sqrt{2-{x^2}}$的两个不同的交点,则实数a的取值范围是( )
| A. | (-2,2) | B. | (0,2) | C. | $({\sqrt{2},2})$ | D. | $[{\sqrt{2},2})$ |
7.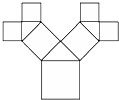 如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )
如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )
 如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )
如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )| A. | $\frac{1}{64}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{8}$ |
8.已知集合U=R,A={x|-1<x<10},B={x|x-4≥0},则A∩∁UB=( )
| A. | {x|-1<x<4} | B. | {x|-1<x≤4} | C. | {x|4≤x<10} | D. | {x|-1≤x≤4} |