题目内容
16.在△ABC中,角A,B,C所对的边分别是a、b、c,已知b=2,且cos2B+cosB+cos(A-C)=1,当a+2c取得最小值时,最大边所对角的余弦值是-$\frac{\sqrt{2}}{4}$.分析 使用二倍角公式和两角和的余弦函数公式化简,借助于正弦定理得出a,b,c成等比数列,利用基本不等式得出a+2c取得最小值时的条件,代入余弦定理即可求出.
解答 解:在△ABC中,∵cos2B+cosB+cos(A-C)=1,
∴cosB+cos(A-C)=1-cos2B,
∵cosB=-cos(A+C),cos2B=1-2sin2B,
∴cos(A-C)-cos(A+C)=2sin2B,
∴-2sinAsin(-C)=2sin2B,即sinAsinC=sin2B,
∴ac=b2=4.即c=$\frac{4}{a}$.
∴a+2c=a+$\frac{8}{a}$≥2$\sqrt{8}$=4$\sqrt{2}$,当且仅当a=$\frac{8}{a}$即a=2$\sqrt{2}$时取等号.
∴当a+2c取得最小值时,a=2$\sqrt{2}$,c=$\sqrt{2}$.
∴最大边对的角为A,
由余弦定理得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{4+2-8}{4\sqrt{2}}$=-$\frac{\sqrt{2}}{4}$.
故答案为:-$\frac{\sqrt{2}}{4}$.
点评 本题考查了三角函数的恒等变换,正弦定理,余弦定理,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若-$\frac{π}{2}$<θ<0,且P=3cosθ,Q=(cosθ)3,R=${(cosθ)}^{\frac{1}{3}}$,则P,Q,R的大小关系为( )
| A. | R<Q<P | B. | Q<R<P | C. | P<Q<R | D. | R<P<Q |
4.已知矩形ABCD中,AB=4$\sqrt{3}$,BC=4,M,N分别是边BC,CD上的点,且MN=2,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
11.函数f(x)=-|x-2|+ex的零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
1.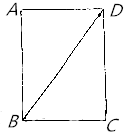 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{8}{25}$ | D. | $\frac{1}{3}$ |
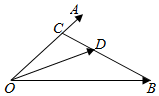 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,C为线段AO上距A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OD}$=$\frac{4}{9}\overrightarrow{a}$$+\frac{1}{3}\overrightarrow{b}$.
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,C为线段AO上距A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OD}$=$\frac{4}{9}\overrightarrow{a}$$+\frac{1}{3}\overrightarrow{b}$.