题目内容
在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
(Ⅰ)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(Ⅱ)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
| 作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| 作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.4 | 0.6 |
(Ⅱ)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
考点:离散型随机变量及其分布列,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)分别求出对应的概率,即可求X的分布列;
(Ⅱ)分别求出3季中有2季的利润不少于2000元的概率和3季中利润不少于2000元的概率,利用概率相加即可得到结论.
(Ⅱ)分别求出3季中有2季的利润不少于2000元的概率和3季中利润不少于2000元的概率,利用概率相加即可得到结论.
解答:
解:(Ⅰ)设A表示事件“作物产量为300kg”,B表示事件“作物市场价格为6元/kg”,
则P(A)=0.5,P(B)=0.4,
∵利润=产量×市场价格-成本,
∴X的所有值为:
500×10-1000=4000,500×6-1000=2000,
300×10-1000=2000,300×6-1000=800,
则P(X=4000)=P(
)P(
)=(1-0.5)×(1-0.4)=0.3,
P(X=2000)=P(
)P(B)+P(A)P(
)=(1-0.5)×0.4+0.5(1-0.4)=0.5,
P(X=800)=P(A)P(B)=0.5×0.4=0.2,
则X的分布列为:
(Ⅱ)设Ci表示事件“第i季利润不少于2000元”(i=1,2,3),
则C1,C2,C3相互独立,
由(Ⅰ)知,P(Ci)=P(X=4000)+P(X=2000)=0.3+0.5=0.8(i=1,2,3),
3季的利润均不少于2000的概率为P(C1C2C3)=P(C1)P(C2)P(C3)=0.83=0.512,
3季的利润有2季不少于2000的概率为P(
C2C3)+P(C1
C3)+P(C1C2
)=3×0.82×0.2=0.384,
综上:这3季中至少有2季的利润不少于2000元的概率为:0.512+0.384=0.896.
则P(A)=0.5,P(B)=0.4,
∵利润=产量×市场价格-成本,
∴X的所有值为:
500×10-1000=4000,500×6-1000=2000,
300×10-1000=2000,300×6-1000=800,
则P(X=4000)=P(
. |
| A |
. |
| B |
P(X=2000)=P(
. |
| A |
. |
| B |
P(X=800)=P(A)P(B)=0.5×0.4=0.2,
则X的分布列为:
| X | 4000 | 2000 | 800 |
| P | 0.3 | 0.5 | 0.2 |
则C1,C2,C3相互独立,
由(Ⅰ)知,P(Ci)=P(X=4000)+P(X=2000)=0.3+0.5=0.8(i=1,2,3),
3季的利润均不少于2000的概率为P(C1C2C3)=P(C1)P(C2)P(C3)=0.83=0.512,
3季的利润有2季不少于2000的概率为P(
. |
| C1 |
. |
| C2 |
. |
| C3 |
综上:这3季中至少有2季的利润不少于2000元的概率为:0.512+0.384=0.896.
点评:本题主要考查随机变量的分布列及其概率的计算,考查学生的计算能力.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
设函数f(x)=x3-4x+a(a>0),若f(x)的三个零点分别为x1,x2,x3,且x1<x2<x3,则( )
| A、x1>-2 | ||
B、x12+x22<
| ||
| C、x3>2 | ||
D、x22+x32<
|

 如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点.
如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点.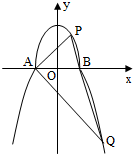 如图,曲线C由上半椭圆C1:
如图,曲线C由上半椭圆C1: 如图1,四面体ABCD及其三视图(如图2所示),过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.
如图1,四面体ABCD及其三视图(如图2所示),过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.