题目内容
设△ABC重心为G,∠A,∠B,∠C的对边分别为a,b,c,若a
+
b
+
c
=
,则∠C= .
| GA |
| 3 |
| 5 |
| GB |
| 3 |
| 7 |
| GC |
| 0 |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:△ABC重心为G,可得
+
+
=
,代入a
+
b
+
c
=
,整理为(
b-a)
=(a-
c)
.由G为△ABC重心,可知:
与
不可能共线.可得
b-a=a-
c=0,再利用余弦定理即可得出.
| GA |
| GB |
| GC |
| 0 |
| GA |
| 3 |
| 5 |
| GB |
| 3 |
| 7 |
| GC |
| 0 |
| 3 |
| 5 |
| GB |
| 3 |
| 7 |
| GC |
| GB |
| GC |
| 3 |
| 5 |
| 3 |
| 7 |
解答:
解:∵△ABC重心为G,
∴
+
+
=
,
∴
=-(
+
),
∵a
+
b
+
c
=
,
∴-a(
+
)+
b
+
c
=
,
化为(
b-a)
=(a-
c)
,
∵G为△ABC重心,
∴
与
不可能共线.
∴
b-a=a-
c=0,
∴a=
c,b=
c.
由余弦定理可得:cosC=
=
=-
,
∵C∈(0,π),
∴C=
.
故答案为:
.
∴
| GA |
| GB |
| GC |
| 0 |
∴
| GA |
| GB |
| GC |
∵a
| GA |
| 3 |
| 5 |
| GB |
| 3 |
| 7 |
| GC |
| 0 |
∴-a(
| GB |
| GC |
| 3 |
| 5 |
| GB |
| 3 |
| 7 |
| GC |
| 0 |
化为(
| 3 |
| 5 |
| GB |
| 3 |
| 7 |
| GC |
∵G为△ABC重心,
∴
| GB |
| GC |
∴
| 3 |
| 5 |
| 3 |
| 7 |
∴a=
| 3 |
| 7 |
| 5 |
| 7 |
由余弦定理可得:cosC=
| a2+b2-c2 |
| 2ab |
(
| ||||
2×
|
| 1 |
| 2 |
∵C∈(0,π),
∴C=
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题考查了三角形重心性质、余弦定理、向量共线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
椭圆
+y2=1两个焦点分别是F1,F2,点P是椭圆上任意一点,则
•
的取值范围是( )
| x2 |
| 4 |
| PF1 |
| PF2 |
| A、[1,4] |
| B、[1,3] |
| C、[-2,1] |
| D、[-1,1] |
函数f(x)=2x3-6x的“临界点”是( )
| A、1 | B、-1 | C、-1和1 | D、0 |
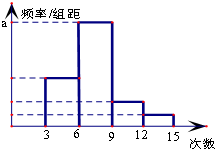 对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: