题目内容
19．已知三棱锥的所有棱长均为$\sqrt{2}$，则该三棱锥的外接球的直径为$\sqrt{3}$．分析 由正三棱锥S-ABC的所有棱长均为$\sqrt{2}$，所以此三棱锥一定可以放在棱长为1的正方体中，所以此四面体的外接球即为此正方体的外接球，由此能求出此四面体的外接球的直径．
解答 解：∵正三棱锥的所有棱长均为$\sqrt{2}$，
∴此三棱锥一定可以放在正方体中，
∴我们可以在正方体中寻找此三棱锥．
∴正方体的棱长为1，
∴此四面体的外接球即为此正方体的外接球，
∵外接球的直径为正方体的对角线长$\sqrt{3}$，
故答案为：$\sqrt{3}$．
点评 本题考查几何体的接体问题，考查了空间想象能力，其解答的关键是根据几何体的结构特征，放在正方体中求解．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
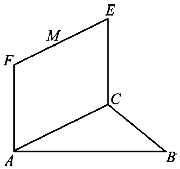如图，矩形ACEF和等边三角形ABC中，AC=2，CE=1，平面ABC⊥平面ACEF．
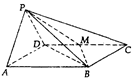如图，在四棱锥中P-ABCD中，底面ABCD是菱形，且∠DAB=60°，PA=PD，M为CD的中点，平面PAD⊥平面ABCD．
11．设复数z满足（1+i）z=|1-i|（i为虚数单位），则$\overline z$=（ ）
| A． | 1+i | B． | 1-i | C． | $\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}i$ | D． | $\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{2}i$ |
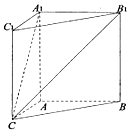如图，在三棱柱ABC-A1B1C1中，四边形AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．