题目内容
19．已知函数f（x）=$\left\{\begin{array}{l}{x（x-a），x≥a}\\{x（a-x），x＜a}\end{array}\right.$，（1）当a=2时解不等式f（x）＜x；
（2）当a＞0时解关于x的不等式f（x）＜2a2．
分析 （1）将a=2代入，分别解出不同情况满足不等式f（x）＜x的x值，综合可得答案；
（2）分别求解不同情况下满足不等式f（x）＜2a2的x值，综合可得答案；
解答 解：（1）当a=2时，不等式f（x）＜x可化为：
$\left\{\begin{array}{l}x（x-2）＜x，x≥2\\ x（2-x）＜x，x＜2\end{array}\right.$
解得：x∈（-∞，0）∪（1，3）；
（2）当a＞0时，2a＞a，
等式f（x）＜2a2可化为：
$\left\{\begin{array}{l}x（x-a）＜2{a}^{2}，x≥a\\ x（a-x）＜2{a}^{2}，x＜a\end{array}\right.$，
当x≥a时，不等式可化为：x2-ax-2a2＜0，
解得：-a＜x＜2a，
∴a≤x＜2a，
当x＜a时，不等式可化为：x2-ax+2a2＞0，
此时不等式恒成立，
∴x＜a，
综上可得：原不等式的解集为（-∞，2a）
点评 本题考查的知识点是分段函数的应用，二次不等式的解法，二次函数的图象和性质，难度中档．
练习册系列答案
相关题目
7．
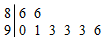如图是某班8为学生诗词比赛得分的茎叶图，那么这8为学生得分的众数和中位数分别为（ ）
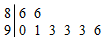如图是某班8为学生诗词比赛得分的茎叶图，那么这8为学生得分的众数和中位数分别为（ ）| A． | 93，91 | B． | 86，93 | C． | 93，92 | D． | 86，91 |
14．从2016年3月8日起，进行自主招生的高校陆续公布招生简章，某市教育部门为了调查几所重点高中的学生参加今年自主招生的情况，选取了文科生与理科生的同学作为调查对象，进行了问卷调查，其中，“参加自主招生”、“不参加自主招生”和“待定”的人数如表：
（1）在所有参加调查的同学中，用分层抽样方法抽取n人，其中“参加自主招生”的同学共36人，求n的值；
（2）在“不参加自主招生”的同学中仍然用分层抽样方法抽取5人，从这5人中任意抽取2人，求至少有一个是理科生的概率．
| 参加 | 不参加 | 待定 | |
| 文科生 | 120 | 300 | 180 |
| 理科生 | 780 | 200 | 420 |
（2）在“不参加自主招生”的同学中仍然用分层抽样方法抽取5人，从这5人中任意抽取2人，求至少有一个是理科生的概率．
4．2015年秋季开学之际，某校高一数学老师为了解学生的计算能力，先给出了一组计算测试题，全校学生完成时间在[20，40）（单位：分钟），各区间学生频率如下表：
若全校共有高一新生1000人．
（1）若学校规定完成时间不低于30分钟的要进行强化训练，试试估计全校参加强化训练的学生人数；
（2）若从全校按照完成时间，利用分层抽样的方法抽取10人．
①若从抽取的这10人中随机抽取1人，求他完成时间恰好在[30，40）的概率；
②若一节课为45分钟，从开始上课即进行测试，从这10人中随机抽取2人，求这两人所用测试时间都不超过30分钟的概率．
| 完成时间 | 频率 |
| [20，25） | 0.2 |
| [25，30） | 0.5 |
| [30，35） | 0.2 |
| [35，40） | 0.1 |
（1）若学校规定完成时间不低于30分钟的要进行强化训练，试试估计全校参加强化训练的学生人数；
（2）若从全校按照完成时间，利用分层抽样的方法抽取10人．
①若从抽取的这10人中随机抽取1人，求他完成时间恰好在[30，40）的概率；
②若一节课为45分钟，从开始上课即进行测试，从这10人中随机抽取2人，求这两人所用测试时间都不超过30分钟的概率．