题目内容
已知G是三角形ABC的重心,过G的直线分别交直线AB,AC于M,N两点,
=m
,
=n
,(m,n都是正数),
+
的最小值是( )
| AB |
| AM |
| AC |
| AN |
| 1 |
| m |
| 2 |
| n |
| A、2 | ||||
| B、3 | ||||
| C、1 | ||||
D、1+
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:由于M,N,G三点共线,利用向量共线定理可得:存在实数λ使得
=λ
+(1-λ)
,利用
=m
,
=n
,(m,n都是正数),可得
=
+
.由于G是三角形ABC的重心,可得
=
+
.根据平面向量基本定理可得
,化为m+n=3.再利用“乘1法”和基本不等式的性质即可得出.
| AG |
| AM |
| AN |
| AB |
| AM |
| AC |
| AN |
| AG |
| λ |
| m |
| AB |
| 1-λ |
| n |
| AC |
| AG |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
|
解答:
解:如图所示,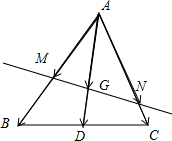
设D是BC的中点.
∵M,N,G三点共线,
∴存在实数λ使得
=λ
+(1-λ)
,
∵
=m
,
=n
,(m,n都是正数),
∴
=
+
,
∵G是三角形ABC的重心,
∴
=
=
×
(
+
)=
+
.
∴
,化为m+n=3.
又m,n为正数,
∴
+
=
(m+n)(
+
)=
(3+
+
)≥
(3+2
)=1+
,当且仅当n=
m=3(
-1)时取等号.
∴
+
的最小值是1+
.
故选:D.

设D是BC的中点.
∵M,N,G三点共线,
∴存在实数λ使得
| AG |
| AM |
| AN |
∵
| AB |
| AM |
| AC |
| AN |
∴
| AG |
| λ |
| m |
| AB |
| 1-λ |
| n |
| AC |
∵G是三角形ABC的重心,
∴
| AG |
| 2 |
| 3 |
| AD |
| 2 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
∴
|
又m,n为正数,
∴
| 1 |
| m |
| 2 |
| n |
| 1 |
| 3 |
| 1 |
| m |
| 2 |
| n |
| 1 |
| 3 |
| n |
| m |
| 2m |
| n |
| 1 |
| 3 |
|
2
| ||
| 3 |
| 2 |
| 2 |
∴
| 1 |
| m |
| 2 |
| n |
2
| ||
| 3 |
故选:D.
点评:本题考查了向量共线定理、三角形的重心定理、向量的平行四边形法则、“乘1法”和基本不等式的性质等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
复数z=i(1+i)(i是虚数单位)的共轭复数
在复平面内对应的点在( )
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中,a=2011,b=1,则sinA:sinB等于( )
| A、1:1 | B、1:2011 |
| C、2011:1 | D、不确定 |
直线3x+y-3=0与直线6x+my+1=0平行,则m的值为( )
| A、2 | B、-2 | C、18 | D、-18 |
在△ABC中,a,b,c分别是角A,B,C的对边,且a:b:c=
:1:2,则角B为( )
| 3 |
| A、30° | B、60° |
| C、90° | D、120° |
已知AD、BE分别是△ABC的边BC,AC上的中线,且
=
,
=
,则
=( )
| AD |
| a |
| BE |
| b |
| BC |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知|
|=2,|
|≠0,且函数f(x)=
x3+
|
|x2+
•
x在R上有极值,则
与
的夹角范围为( )
| a |
| b |
| 1 |
| 3 |
| 1 |
| 2 |
| a |
| a |
| b |
| a |
| b |
A、[0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
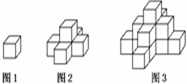 如图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是
如图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是